
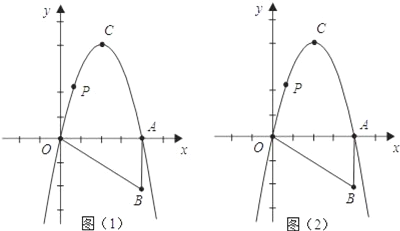
ЎҫМвДҝЎҝИзНјЈ¬RtЎчOABИзНјЛщКҫ·ЕЦГФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ЦұҪЗұЯOAУлxЦбЦШәПЈ¬ЎПOAB=90ЎгЈ¬OA=4Ј¬AB=2Ј¬°СRtЎчOABИЖөгOДжКұХлРэЧӘ90ЎгЈ¬өгBРэЧӘөҪөгCөДО»ЦГЈ¬Т»МхЕЧОпПЯХэәГҫӯ№эөгOЈ¬CЈ¬AИэөгЈ®
ЈЁ1Ј©ЗуёГЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ2Ј©ФЪxЦбЙП·ҪөДЕЧОпПЯЙПУРТ»¶ҜөгPЈ¬№эөгPЧчxЦбөДЖҪРРПЯҪ»ЕЧОпПЯУЪөгMЈ¬·Цұр№эөгPЈ¬өгMЧчxЦбөДҙ№ПЯЈ¬Ҫ»xЦбУЪEЈ¬FБҪөгЈ¬ОКЈәЛДұЯРОPEFMөДЦЬіӨКЗ·сУРЧоҙуЦөЈҝИз№ыУРЈ¬ЗлЗуіцЧоЦөЈ¬ІўРҙіцҪвҙр№эіМЈ»Из№ыГ»УРЈ¬ЗлЛөГчАнУЙЈ®
ЈЁ3Ј©Из№ыxЦбЙПУРТ»¶ҜөгHЈ¬ФЪЕЧОпПЯЙПКЗ·сҙжФЪөгNЈ¬К№OЈЁФӯөгЈ©ЎўCЎўHЎўNЛДөг№№іЙТФOCОӘТ»ұЯөДЖҪРРЛДұЯРОЈҝИфҙжФЪЈ¬ЗуіцNөгөДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ўҫҙр°ёЎҝ(1)Ўўy=©Ғx2+4xЈ»(2)Ўў10Ј»(3)ЎўN1ЈЁ2+2![]() Ј¬©Ғ4Ј©Ј¬N2ЈЁ2©Ғ2
Ј¬©Ғ4Ј©Ј¬N2ЈЁ2©Ғ2![]() Ј¬©Ғ4Ј©
Ј¬©Ғ4Ј©
ЎҫҪвОцЎҝКФМв·ЦОцЈә(1)ЎўёщҫЭРэЧӘөДРФЦКҝЙЗуіцCөДЧшұкәНAөДЧшұкЈ¬УЦТтОӘЕЧОпПЯҫӯ№эФӯөгЈ¬№КЙиy=ax2+bx°СЈЁ2Ј¬4Ј©Ј¬ЈЁ4Ј¬0Ј©ҙъИлЈ¬ЗуіцaәНbөДЦөјҙҝЙЗуіцёГЕЧОпПЯөДҪвОцКҪЈ»(2)ЎўЛДұЯРОPEFMөДЦЬіӨУРЧоҙуЦөЈ¬ЙиөгPөДЧшұкОӘPЈЁaЈ¬©Ғa2+4aЈ©ФтУЙЕЧОпПЯөД¶ФіЖРФЦӘOE=AFЈ¬ЛщТФEF=PM=4©Ғ2aЈ¬PE=MF=©Ғa2+4aЈ¬ФтҫШРОPEFMөДЦЬіӨL=2[4©Ғ2a+ЈЁ©Ғa2+4aЈ©]=©Ғ2ЈЁa©Ғ1Ј©2+10Ј¬АыУГәҜКэөДРФЦКјҙҝЙЗуіцЛДұЯРОPEFMөДЦЬіӨөДЧоҙуЦөЈ»(3)ЎўФЪЕЧОпПЯЙПҙжФЪөгNЈ¬К№OЈЁФӯөгЈ©ЎўCЎўHЎўNЛДөг№№іЙТФOCОӘТ»ұЯөДЖҪРРЛДұЯРОЈ¬УЙЈЁ1Ј©ҝЙЗуіцЕЧОпПЯөД¶ҘөгЧшұкЈ¬№эөгCЧчxЦбөДЖҪРРПЯЈ¬УлxЦбГ»УРЖдЛьҪ»өгЈ¬№эy=©Ғ4ЧчxЦбөДЖҪРРПЯЈ¬УлЕЧОпПЯУРБҪёцҪ»өгЈ¬ХвБҪёцҪ»өгОӘЛщЗуөДNөгЧшұкЛщТФУР©Ғx2+4x=©Ғ4Ј¬Ҫв·ҪіМјҙҝЙЗуіцҪ»өгЧшұкЈ®
КФМвҪвОцЈә(1)ЎўТтОӘOA=4Ј¬AB=2Ј¬°СЎчAOBИЖөгOДжКұХлРэЧӘ90ЎгЈ¬
ҝЙТФИ·¶ЁөгCөДЧшұкОӘЈЁ2Ј¬4Ј©Ј»УЙНјҝЙЦӘөгAөДЧшұкОӘЈЁ4Ј¬0Ј©Ј¬
УЦТтОӘЕЧОпПЯҫӯ№эФӯөгЈ¬№КЙиy=ax2+bx°СЈЁ2Ј¬4Ј©Ј¬ЈЁ4Ј¬0Ј©ҙъИлЈ¬өГ![]() Ј¬ҪвөГ
Ј¬ҪвөГ![]()
ЛщТФЕЧОпПЯөДҪвОцКҪОӘy=©Ғx2+4xЈ»
(2)ЎўЛДұЯРОPEFMөДЦЬіӨУРЧоҙуЦөЈ¬АнУЙИзПВЈә
УЙМвТвЈ¬ИзНјЛщКҫЈ¬ЙиөгPөДЧшұкОӘPЈЁaЈ¬©Ғa2+4aЈ©ФтУЙЕЧОпПЯөД¶ФіЖРФЦӘOE=AFЈ¬
ЎаEF=PM=4©Ғ2aЈ¬PE=MF=©Ғa2+4aЈ¬
ФтҫШРОPEFMөДЦЬіӨL=2[4©Ғ2a+ЈЁ©Ғa2+4aЈ©]=©Ғ2ЈЁa©Ғ1Ј©2+10Ј¬
Ўаөұa=1КұЈ¬ҫШРОPEFMөДЦЬіӨУРЧоҙуЦөЈ¬Lmax=10Ј»
(3)ЎўФЪЕЧОпПЯЙПҙжФЪөгNЈ¬К№OЈЁФӯөгЈ©ЎўCЎўHЎўNЛДөг№№іЙТФOCОӘТ»ұЯөДЖҪРРЛДұЯРОЈ¬АнУЙИзПВЈә
ЎЯy=©Ғx2+4x=©ҒЈЁx©Ғ2Ј©2+4ҝЙЦӘ¶ҘөгЧшұкЈЁ2Ј¬4Ј©Ј¬
ЎаЦӘөАCөгХэәГКЗ¶ҘөгЧшұкЈ¬ЦӘөАCөгөҪxЦбөДҫаАлОӘ4ёцөҘО»іӨ¶ИЈ¬
№эөгCЧчxЦбөДЖҪРРПЯЈ¬УлxЦбГ»УРЖдЛьҪ»өгЈ¬№эy=©Ғ4ЧчxЦбөДЖҪРРПЯЈ¬УлЕЧОпПЯУРБҪёцҪ»өгЈ¬
ХвБҪёцҪ»өгОӘЛщЗуөДNөгЧшұкЛщТФУР©Ғx2+4x=©Ғ4 ҪвөГx1=2+![]() Ј¬x2=2©Ғ
Ј¬x2=2©Ғ![]()
ЎаNөгЧшұкОӘN1ЈЁ2+![]() Ј¬©Ғ4Ј©Ј¬N2ЈЁ2©Ғ
Ј¬©Ғ4Ј©Ј¬N2ЈЁ2©Ғ![]() Ј¬©Ғ4Ј©Ј®
Ј¬©Ғ4Ј©Ј®


 СѧѧϰәГ°пКЦПөБРҙр°ё
СѧѧϰәГ°пКЦПөБРҙр°ё РЎС§Н¬ІҪИэБ·әЛРДГЬҫнПөБРҙр°ё
РЎС§Н¬ІҪИэБ·әЛРДГЬҫнПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҪв·ҪіМЈә
ЈЁ1Ј©4ЈЁx©Ғ2Ј©2©Ғ49=0Ј®
ЈЁ2Ј©x2©Ғ5x©Ғ7=0Ј®
ЈЁ3Ј©ЈЁ2x+1Ј©ЈЁx©Ғ2Ј©=3Ј®
ЈЁ4Ј©3xЈЁx©Ғ2Ј©=2ЈЁ2©ҒxЈ©Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝКэС§»о¶ҜҝОЙПЈ¬АПКҰМбіцБЛТ»ёцОКМвЈә
ИзНј1Ј¬AЎўBБҪөгұ»іШМБёфҝӘЈ¬ФЪABНвСЎТ»өгЈ¬Б¬ҪУACәНBCЈ¬ФхСщІвіцAЎўBБҪөгөДҫаАлЈҝ

Ўҫ»о¶ҜМҪҫҝЎҝС§ЙъТФРЎЧйХ№ҝӘМЦВЫЈ¬ЧЬҪбіцТФПВ·Ҫ·ЁЈә
ЈЁ1Ј©ИзНј2Ј¬СЎИЎөгCЈ¬К№AC=BC=aЈ¬ЎПC=60ЎгЈ»
ЈЁ2Ј©ИзНј3Ј¬СЎИЎөгCЈ¬К№AC=BC=bЈ¬ЎПC=90ЎгЈ»
ЈЁ3Ј©ИзНј4Ј¬СЎИЎөгCЈ¬Б¬ҪУACЈ¬BCЈ¬И»әуИЎACЎўBCөДЦРөгDЎўEЈ¬БҝөГDE=cЎӯ
Ўҫ»о¶ҜЧЬҪбЎҝ
ЈЁ1Ј©ЗлёщҫЭЙПКцИэЦЦ·Ҫ·ЁЈ¬ТАҙОРҙіцAЎўBБҪөгөДҫаАлЈ®ЈЁУГә¬ЧЦДёөДҙъКэКҪұнКҫЈ©ІўРҙіц·Ҫ·ЁЈЁ3Ј©ЛщёщҫЭөД¶ЁАнЈ®
AB= Ј¬AB= ![]() b Ј¬AB= Ј®
b Ј¬AB= Ј®
¶ЁАнЈә Ј®
ЈЁ2Ј©ЗлДгФЩЙијЖТ»ЦЦІвБҝ·Ҫ·ЁЈ¬ЈЁНј5Ј©»ӯіцНјРОЈ¬јтТӘЛөГч№эіМј°Ҫб№ыјҙҝЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
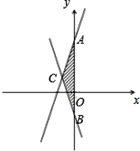
ЎҫМвДҝЎҝТСЦӘЈ¬ЦұПЯ y=2x+3 УлЦұПЯ y= ©Ғ 2x ©Ғ 1.
ЈЁ 1 Ј©ЗуБҪЦұПЯУл y ЦбҪ»өгAЈ¬BөДЧшұкЈ»
ЈЁ 2 Ј©ЗуБҪЦұПЯҪ»өг C өДЧшұкЈ»
ЈЁ 3 Ј©Зу Ўч ABC өДГж»эЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіРЈҝӘХ№БЛЎ°»ҘЦъЎўЖҪөИЎўёР¶чЎўәНРіЎўҪшИЎЎұЦчМв°а»б»о¶ҜЈ¬»о¶ҜәуЈ¬ҫН»о¶ҜөД![]() ёцЦчМвҪшРРБЛійСщөчІйЈЁГҝО»Н¬С§Ц»СЎЧо№ШЧўөДТ»ёцЈ©Ј¬ёщҫЭөчІйҪб№ы»жЦЖБЛБҪ·щІ»НкХыөДНіјЖНјЈ®ёщҫЭНјЦРМṩөДРЕПўЈ¬ҪвҙрПВБРОКМвЈә
ёцЦчМвҪшРРБЛійСщөчІйЈЁГҝО»Н¬С§Ц»СЎЧо№ШЧўөДТ»ёцЈ©Ј¬ёщҫЭөчІйҪб№ы»жЦЖБЛБҪ·щІ»НкХыөДНіјЖНјЈ®ёщҫЭНјЦРМṩөДРЕПўЈ¬ҪвҙрПВБРОКМвЈә
ЈЁ1Ј©ХвҙОөчІйөДС§Йъ№ІУР¶аЙЩГыЈҝ
ЈЁ2Ј©ЗлҪ«МхРОНіјЖНјІ№ідНкХыЈ¬ІўФЪЙИРОНіјЖНјЦРјЖЛгіцЎ°ҪшИЎЎұЛщ¶ФУҰөДФІРДҪЗөД¶ИКэЈ®
ЈЁ3Ј©Из№ыТӘФЪХв![]() ёцЦчМвЦРИОСЎБҪёцҪшРРөчІйЈ¬ёщҫЭЈЁ2Ј©ЦРөчІйҪб№ыЈ¬УГКчЧҙНј»тБРұн·ЁЈ¬ЗуЗЎәГСЎөҪС§Йъ№ШЧўЧо¶аөДБҪёцЦчМвөДёЕВКЈЁҪ«»ҘЦъЎўЖҪөИЎўёР¶чЎўәНРіЎўҪшИЎТАҙОјЗОӘAЎўBЎўCЎўDЎўEЈ©Ј®
ёцЦчМвЦРИОСЎБҪёцҪшРРөчІйЈ¬ёщҫЭЈЁ2Ј©ЦРөчІйҪб№ыЈ¬УГКчЧҙНј»тБРұн·ЁЈ¬ЗуЗЎәГСЎөҪС§Йъ№ШЧўЧо¶аөДБҪёцЦчМвөДёЕВКЈЁҪ«»ҘЦъЎўЖҪөИЎўёР¶чЎўәНРіЎўҪшИЎТАҙОјЗОӘAЎўBЎўCЎўDЎўEЈ©Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ABЎОCDЈ¬ЎПABKөДҪЗЖҪ·ЦПЯBEөД·ҙПтСУіӨПЯәНЎПDCKөДҪЗЖҪ·ЦПЯCFөД·ҙПтСУіӨПЯҪ»УЪөгHЈ¬ЎПK©ҒЎПH=27ЎгЈ¬ФтЎПK=ЈЁЎЎЎЎЈ©

A. 76Ўг B. 78Ўг C. 80Ўг D. 82Ўг
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪҫШРОABCDЦРЈ¬OОӘACЦРөгЈ¬EF№эOөгЗТEFЎНAC·ЦұрҪ»DCУЪFЈ¬Ҫ»ABУЪөгEЈ¬өгGКЗAEЦРөгЗТЎПAOG=30ЎгЈ¬ФтПВБРҪбВЫХэИ·өДёцКэОӘЈЁ Ј©
ЈЁ1Ј©DC=3OGЈ» ЈЁ2Ј©OG=![]() BCЈ» ЈЁ 3Ј©OGEКЗөИұЯИэҪЗРОЈ» ЈЁ 4Ј©SAOE=
BCЈ» ЈЁ 3Ј©OGEКЗөИұЯИэҪЗРОЈ» ЈЁ 4Ј©SAOE= ![]() SҫШРОABCD
SҫШРОABCD
A. 1
B. 2
C. 3
D. 4
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪБвРОABCDЦРЈ¬AEЎНBCУЪөгEЈ¬AFЎНCDУЪөгFЈ¬ЗТEЎўF·ЦұрОӘBCЎўCDөДЦРөгЈ¬ЈЁИзНјЈ©ФтЎПEAFөИУЪЈЁЎЎЎЎЈ©
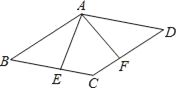
A. 75ЎгB. 45ЎгC. 60ЎгD. 30Ўг
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
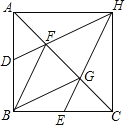
ЎҫМвДҝЎҝТСЦӘЈәИзНјЈ¬ФЪЎчABCЦРЈ¬AB=BCЈ¬ЎПABC=90ЎгЈ¬өгDЎўE·ЦұрКЗұЯABЎўBCөДЦРөгЈ¬өгFЎўGКЗұЯACөДИэөИ·ЦөгЈ¬DFЎўEGөДСУіӨПЯПаҪ»УЪөгHЈ¬Б¬ҪУHAЎўHCЈ®
(1)ЗуЦӨЈәЛДұЯРОFBGHКЗБвРОЈ»
(2)ЗуЦӨЈәЛДұЯРОABCHКЗХэ·ҪРОЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com