
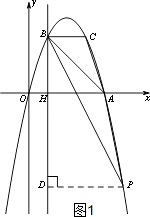
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
【答案】
(1)
解:把点A(4,0),B(1,3)代入抛物线y=ax2+bx中,
得 ![]() 解得:
解得: ![]() ,
,
∴抛物线表达式为:y=﹣x2+4x;
(2)
解:点C的坐标为(3,3),
又∵点B的坐标为(1,3),
∴BC=2,
∴S△ABC= ![]() ×2×3=3;
×2×3=3;
(3)
解:过P点作PD⊥BH交BH于点D,
设点P(m,﹣m2+4m),
根据题意,得:BH=AH=3,HD=m2﹣4m,PD=m﹣1,
∴S△ABP=S△ABH+S四边形HAPD﹣S△BPD,
6= ![]() ×3×3+
×3×3+ ![]() (3+m﹣1)(m2﹣4m)﹣
(3+m﹣1)(m2﹣4m)﹣ ![]() (m﹣1)(3+m2﹣4m),
(m﹣1)(3+m2﹣4m),
∴3m2﹣15m=0,
m1=0(舍去),m2=5,
∴点P坐标为(5,﹣5).
(4)
解:以点C、M、N为顶点的三角形为等腰直角三角形时,分三类情况讨论:
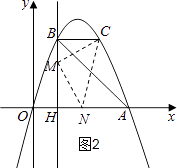
①以点M为直角顶点且M在x轴上方时,如图2,CM=MN,∠CMN=90°,
则△CBM≌△MHN,
∴BC=MH=2,BM=HN=3﹣2=1,
∴M(1,2),N(2,0),
由勾股定理得:MC= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =
= ![]() ;
;
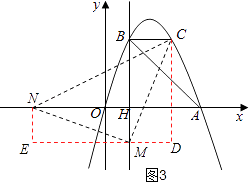
②以点M为直角顶点且M在x轴下方时,如图3,作辅助线,构建如图所示的两直角三角形:Rt△NEM和Rt△MDC,
得Rt△NEM≌Rt△MDC,
∴EM=CD=5,MD=ME=2,
由勾股定理得:CM= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =
= ![]() ;
;
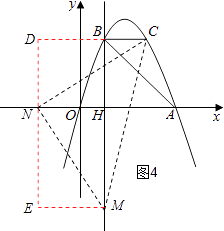
③以点N为直角顶点且N在y轴左侧时,如图4,CN=MN,∠MNC=90°,作辅助线,
同理得:CN= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =17;
=17;
④以点N为直角顶点且N在y轴右侧时,作辅助线,如图5,同理得:CN= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =5;
=5;
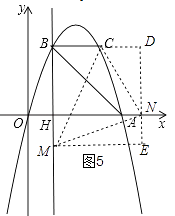
⑤以C为直角顶点时,不能构成满足条件的等腰直角三角形;
综上所述:△CMN的面积为: ![]() 或
或 ![]() 或17或5.
或17或5.
【解析】本题是二次函数的综合题,考查了利用待定系数法求二次函数的表达式,考查了等腰直角三角形和全等三角形的判定和性质;本题的一般思路为:①根据函数的表达式设出点的坐标,利用面积公式直接表示或求和或求差列式,求出该点的坐标;②利用等腰直角三角形的两直角边相等,构建两直角三角形全等,再利用全等性质与点的坐标结合解决问题.(1)利用待定系数法求二次函数的表达式;(2)根据二次函数的对称轴x=2写出点C的坐标为(3,3),根据面积公式求△ABC的面积;(3)因为点P是抛物线上一动点,且位于第四象限,设出点P的坐标(m,﹣m2+4m),利用差表示△ABP的面积,列式计算求出m的值,写出点P的坐标;(4)分别以点C、M、N为直角顶点分三类进行讨论,利用全等三角形和勾股定理求CM或CN的长,利用面积公式进行计算.
【考点精析】关于本题考查的等腰直角三角形,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
(进价、售价均保持不变,利润 = 销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;

(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,匀速行驶,设慢车行驶的时间x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象回答:
(1)甲、乙两地之间的距离为 ;
(2)两车同时出发后 h相遇;
(3)慢车的速度为 千米/小时;快车的速度为 千米/小时;
(4)线段CD表示的实际意义是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用代数式表示:
(1)比a与b的和小3的数.
(2)比a与b的差的一半大1的数.
(3)比a除以b的商的3倍大8的数.
(4)比a除b的商的3倍大8的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.关系:①AD∥BC;②AB=CD;③∠A=∠C;④∠B+∠C=180°.
(1)写出所有成立的情况(只需填写序号);
(2)选择其中一种证明.
已知:在四边形ABCD中, ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.
(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
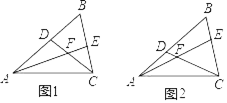
【题目】在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
(1)如图1,若AE、CD为△ABC的角平分线:
①求∠AFD的度数;
②若AD=3,CE=2,求AC的长;
(2)如图2,若∠EAC=∠DCA=30°,求证:AD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p. ![]()
(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com