
【题目】如图,矩形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,且
,且![]() .
.
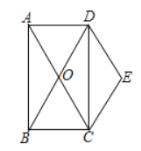
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,求菱形
,求菱形![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据平行四边形的判定得出四边形OCED是平行四边形,根据矩形的性质求出OC=OD,根据菱形的判定得出即可.
(2)解直角三角形求出BC=3,AB=DC=![]() ,连接OE,交CD于点F,根据菱形的性质得出F为CD中点,求出OF=
,连接OE,交CD于点F,根据菱形的性质得出F为CD中点,求出OF=![]() BC=
BC=![]() ,求出OE=2OF=3,求出菱形的面积即可.
,求出OE=2OF=3,求出菱形的面积即可.
解:(1)∵![]() ,
,
∴四边形OCED是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,OC=![]() AC,OD=
AC,OD=![]() BD,
BD,
∴OC=OD,
∴四边形OCED是菱形;
(2)在矩形ABCD中,∠ABC=90°,∠BAC=30°,AC=6,
∴BC=![]() AC=3,
AC=3,
∴AB=DC=![]() ,
,
连接OE,交CD于点F,
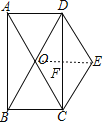
∵四边形ABCD为菱形,
∴F为CD中点,
∵O为BD中点,
∴OF=![]() BC=
BC=![]() ,
,
∴OE=2OF=3,
∴S菱形OCED=![]() ×OE×CD=
×OE×CD=![]() ×3×
×3×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中第九卷《勾股》主要讲述了以测量问题为中心的直角三角形三边互求,之中记载了一道有趣的“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”
译文:“今有正方形水池边长为1丈,有棵芦苇生长在它长出水面的部分为1尺.将芦苇的中央,向池岸牵引,恰好与水岸齐接.问水深,芦苇的长度分别是多少尺?”(备注:1丈=10尺)
如果设水深为![]() 尺,那么芦苇长用含
尺,那么芦苇长用含![]() 的代数式可表示为_______尺,根据题意,可列方程为______________.
的代数式可表示为_______尺,根据题意,可列方程为______________.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.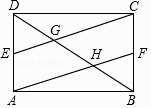
求证:
(1)四边形AFCE是平行四边形;
(2)证明:EG=FH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在平面直角坐标系中,△ABC的位置如图所示:
(1)请写出点A、B、C三点的坐标.
(2)将△ABC向右平移6个单位,再向上平移2个单位,请在图中作出平移后的△A'B'C',并写出它们的坐标:A'( ),B'( ),C'( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,AE⊥BF于点M,求证:AE=BF; 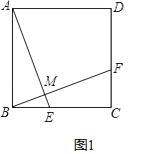
(2)如图2,将 (1)中的正方形ABCD改为矩形ABCD,AB=2,BC=3,AE⊥BF于点M,探究AE与BF的数量关系,并证明你的结论. 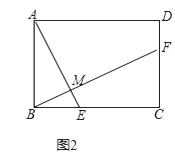
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于两点
轴交于两点![]() 和
和![]() 与
与![]() 轴交于点
轴交于点![]() 动点
动点![]() 沿
沿![]() 的边
的边![]() 以每秒
以每秒![]() 个单位长度的速度由起点
个单位长度的速度由起点![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 的另一边
的另一边![]() 于点
于点![]() 将
将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,设点
处,设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.

(1)求抛物线的解析式;
(2)N为抛物线上的点(点![]() 不与点
不与点![]() 重合)且满足
重合)且满足![]() 直接写出
直接写出![]() 点的坐标;
点的坐标;
(3)是否存在某一时刻![]() ,使
,使![]() 的面积最大,若存在,求出
的面积最大,若存在,求出![]() 的值和最大面积;若不存在,请说明理由.
的值和最大面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)2﹣2+(![]() )0+(﹣0.2)2014×52014
)0+(﹣0.2)2014×52014
(2)(2a3b)3(﹣8ab2)÷(﹣4a4b3)
(3)(2a+1)2﹣(2a+1)(﹣1+2a)
(4)20192﹣2018×2020(运用整式乘法公式进行计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由几个相同的边长为1的小立方块搭成的几何体的俯视图如下图,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个向何体的主视图和左视图.

(2)根据三视图;这个组合几何体的表面积为 _________ 个平方单位.(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大是为 _________ 个平方单位.(包括底面积)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com