
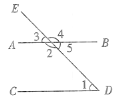
【题目】如图,直线AB,CD被DE所截,则∠1和 是同位角,∠1和 是内错角,∠1和 是同旁内角;
(2)在(1)中,如果∠5=∠1,那么∠1=∠3的推理过程如下,请在括号内注明理由:
因为∠5=∠1( ),
∠5=∠3( ),
所以∠1=∠3( ).
科目:初中数学 来源: 题型:
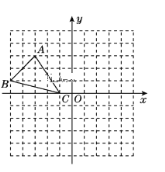
【题目】如图,已知网格上最小的正方形的边长为1,
(1)作△ABC关于![]() 轴的对称图形△A'B'C'(不写做法),并写出A'B'C'的坐标,想一想:关于
轴的对称图形△A'B'C'(不写做法),并写出A'B'C'的坐标,想一想:关于![]() 轴对称的两个点之间有什么关系?
轴对称的两个点之间有什么关系?
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某电脑公司有A型、B型、C型三种型号的电脑,其价格分别为A型每台6 000元,B型每台4 000元,C型每台2 500元,我市东坡中学计划将100 500元钱全部用于该电脑公司购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案供该校选择,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名公关人员,对甲、乙两位候选人进行了面试和笔试,他们的成绩如下表所示:

如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.则( )
A. 甲的平均成绩高于乙的平均成绩
B. 乙的平均成绩高于甲的平均成绩
C. 甲与乙的平均成绩相同
D. 无法确定谁的成绩更高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有10名销售业务员,去年每人完成的销售额情况如表:

(1)求10名销售员销售额的平均数、中位数和众数.(单位:万元)
(2)为了调动员工积极性,公司准备采取超额有奖措施,请问把标准定为多少万元时最合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加社团的情况,从2010年起,某市教育部门每年都从全市所有学生中随机抽取2000名学生进行调查,图①、图②是部分调查数据的统计图(参加社团的学生每人只能报一项)根据统计图提供的信息解决下列

问题:
(1)求图②中“科技类”所在扇形的圆心角α的度数
(2)该市2012年抽取的学生中,参加体育类与理财类社团的学生共有多少人?
(3)该市2014年共有50000名学生,请你估计该市2014年参加社团的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y= ![]() (x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).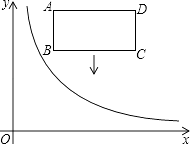
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州地铁5号线全长48.18公里,投资315.9亿元,规划建设预期2014-2019年,杭州工程地铁队负责建设,分两个班组分别从杭州南站外香樟路站和余杭科技岛站同时开工掘进.已知甲组比乙组平均每天多掘进2.4米,经过5天施工,两组共掘进了110米.
(1)求甲、乙两个班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进1.7米,乙组平均每天能比原来多掘进1.3米.按此施工进度,能够比原来少用多少天完成任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com