
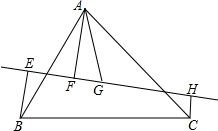
 如图,直线l过△ABC的重心G,它与两边AB、AC相交,设A,B,C在l上的射影分别是F,E,H,求证:BE+CH=AF.
如图,直线l过△ABC的重心G,它与两边AB、AC相交,设A,B,C在l上的射影分别是F,E,H,求证:BE+CH=AF. 分析 连接AG,并延长,交BC于D,过D做DK垂直于直线L,垂足为K,根据三角形中线的性质得到BD=CD,推出BE∥DK∥CH,得到DK为梯开EBCH的中线,求得DK=$\frac{1}{2}$(BE+CH),根据相似三角形的性质得到$\frac{AF}{DK}=\frac{AG}{DG}$=$\frac{1}{2}$,得到AF=2DK,根据得到结论.
解答  证明:连接AG,并延长,交BC于D,过D做DK垂直于直线L,垂足为K,
证明:连接AG,并延长,交BC于D,过D做DK垂直于直线L,垂足为K,
∵直线l过△ABC的重心G,
∴BD=CD,
∵BE⊥直线l,CH⊥直线l,DK⊥直线l,
∴BE∥DK∥CH,
∴DK为梯开EBCH的中线,
∴DK=$\frac{1}{2}$(BE+CH),
∵AF⊥直线l,
∴AF∥DK,
∴△AFG∽△DKG,
∴$\frac{AF}{DK}=\frac{AG}{DG}$=$\frac{1}{2}$,
∴AF=2DK,
∴AF=BE+CH.
点评 本题考查了三角形的重心,相似三角形的判定和性质,梯形的中位线的性质,正确的作出辅助线是解题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
在一个不透明的盒子中,放入2个白球和1个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出2个球,请通过列表或树状图求摸出2个球都是白球的概率;
(2)搅匀后从中任意摸出1个球,记录下颜色后放回袋中,再次搅匀后从中任意摸出1个球,请通过列表或树状图求2次摸出的球都是白球的概率;
(3)现有一个可以自由转动的转盘,转盘被等分成60个相等的扇形,这些扇形除颜色外完全相同,其中40个扇形涂上白色,20个扇形涂上红色,转动转盘2次,指针2次都指向白色区域的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC、BD交于E点,且AB=BD,EC=1,则AD的长是$\frac{3\sqrt{15}}{2}$.
如图,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC、BD交于E点,且AB=BD,EC=1,则AD的长是$\frac{3\sqrt{15}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m2最大 | B. | a最大 | C. | b最大 | D. | c最大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
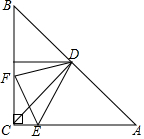 已知△ACB为等腰直角三角形,D为BA的中点,∠EDF=45°,交AC于E点,交BC于F点,连EF.
已知△ACB为等腰直角三角形,D为BA的中点,∠EDF=45°,交AC于E点,交BC于F点,连EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com