

分析 (1)根据三角形内角和定理得到∠BPC=180°-∠PBC-∠PCB,再根据角平分线定义得到∠BPC=180°-($\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB),再利用三角形内角和定理得∠BPC=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A,然后把∠A的度数代入计算;
(2)如图③,结论:∠MPB+∠NPC=90°-$\frac{1}{2}$∠A.根据平角定义得∠MPB+∠NPC=180°-∠BPC,然后根据(1)的求解;
(3)不成立,结论是:∠MPB-∠NPC=90°-$\frac{1}{2}$∠A.由∠MPB=180°-∠BPN=180°-(∠BPC-∠NPC),推出∠MPB-∠NPC=180°-∠BPC=180°-(90°+$\frac{1}{2}$∠A),由此即可证明.
解答 解:(1)如图①
∵在△ABC中,∠A+∠B+∠ACB=180°,且∠A=80°,
∴∠ABC+∠ACB=100°,
∵∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACB,
∴∠1+∠2=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×100°=50°,
∴∠BPC=180°-(∠1+∠2)=180°-50°=130°.
(2)如图③,结论:∠MPB+∠NPC=90°-$\frac{1}{2}$∠A.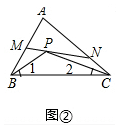
理由:由(1)知:∠BPC=180°-(∠1+∠2);
∵∠1+∠2=$\frac{1}{2}$(180°-∠A)=90°-$\frac{1}{2}$∠A,
∴∠BPC=180°-(90°-$\frac{1}{2}$∠A)=90°+$\frac{1}{2}$∠A;
∴∠MPB+∠NPC=180°-∠BPC=180°-(90°+$\frac{1}{2}$∠A)=90°-$\frac{1}{2}$∠A.
(3)不成立,结论是:∠MPB-∠NPC=90°-$\frac{1}{2}$∠A.
如图③
理由:由(ⅰ)知:∠BPC=90°+$\frac{1}{2}$∠A,
∵∠MPB=180°-∠BPN=180°-(∠BPC-∠NPC),
∴∠MPB-∠NPC=180°-∠BPC=180°-(90°+$\frac{1}{2}$∠A)=90°-$\frac{1}{2}$∠A.
点评 该题主要考查了三角形的内角和定理、角平分线的定义等几何知识点及其应用问题;牢固掌握三角形的内角和定理、角平分线的定义等几何知识点是基础,灵活运用是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:判断题
已知:如图,AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC。
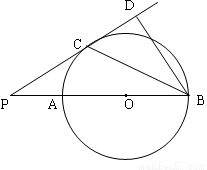
求证:(1)BC平分∠PBD;
(2)BC2=AB·BD。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1的正方形组成的6×5方格中,点A,B都在格点上.
如图,在边长为1的正方形组成的6×5方格中,点A,B都在格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com