
【题目】如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为![]() ,AB=4.
,AB=4.
(1)求点B,P,C的坐标;(2)求证:CD是⊙P的切线.

【答案】(1)B(2,0),P(0,1),C(-2,2);(2)详见解析.
【解析】试题分析:
(1)Rt△OBP中,由勾股定理得到OP的长,连接AC,因为BC是直径,所以∠BAC=90°,因为OP是△ABC的中位线,所以OA=2,AC=2,即可求解;
(2)由点C的坐标可得直线CD的解析式,则可求点D的坐标,从而可用SAS证△DAC≌△POB,进而证∠ACB=90°.
试题解析:
(1)解:如图,连接CA.∵OP⊥AB,∴OB=OA=2.∵OP2+BO2=BP2,
∴OP2=5-4=1,OP=1.∵BC是⊙P的直径,∴∠CAB=90°.
∵CP=BP,OB=OA,∴AC=2OP=2.∴B(2,0),P(0,1),C(-2,2).
(2)证明:∵直线y=2x+b过C点,∴b=6.∴y=2x+6.
∵当y=0时,x=-3,∴D(-3,0).∴AD=1.∵OB=AC=2,AD=OP=1,
∠CAD=∠POB=90°,∴△DAC≌△POB.∴∠DCA=∠ABC.
∵∠ACB+∠CBA=90°,∴∠DCA+∠ACB=90°,即CD⊥BC.∴CD是⊙P的切线.


科目:初中数学 来源: 题型:
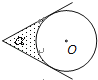
【题目】如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
A. 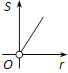 B.
B. 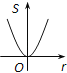 C.
C. 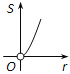 D.
D. 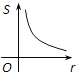
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() .
.
(1)请直接写出点![]() 关于
关于![]() 轴对称的点的坐标;
轴对称的点的坐标;
(2)将![]() 绕坐标原点
绕坐标原点![]() 逆时针旋转90°.画出图形,直接写出点
逆时针旋转90°.画出图形,直接写出点![]() 的对应点的坐标;
的对应点的坐标;
(3)请直接写出:以![]() 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=-![]() x2+bx+c的图象与x轴相交于A(-5,0),B(-1,0).
x2+bx+c的图象与x轴相交于A(-5,0),B(-1,0).
(1)求这个二次函数的关系式;
(2)如果要通过适当的平移,使得这个函数的图象与x轴只有一个交点,那么应该怎样平移?向右还是向左?或者是向上还是向下?应该平移向个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80 m,桥拱到水面的最大高度为20 m.(1)求桥拱的半径.
(2)现有一艘宽60 m,顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
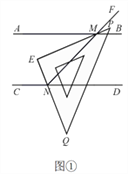
【题目】已知: 两直线![]() ,
,![]() ,且
,且![]() ∥CD,点
∥CD,点![]() ,
,![]() 分别在直线
分别在直线![]() ,
,![]() 上. 放置一个足够大的三角尺,使得三角尺的两边
上. 放置一个足够大的三角尺,使得三角尺的两边![]() ,
,![]() 分别经过点
分别经过点![]() ,
,![]() . 过点
. 过点![]() 作射线
作射线![]() ,使得
,使得![]() .
.
(1)转动三角尺,如图①所示,当射线![]() 与
与![]() 重合,
重合,![]() 时,则
时,则![]() ________;
________;
(2)转动三角尺,如图②所示,当射线![]() 与
与![]() 不重合,
不重合,![]() 时,求
时,求![]() 的度数.
的度数.
(3)转动直角三角尺的过程中, 请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com