
【题目】
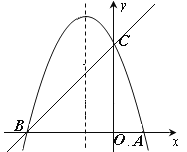
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.
⑴若直线y=mx+n经过B,C两点,求直线BC和抛物线的解析式;
⑵在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求点M的坐标;⑶设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
【答案】(1)![]() ,
,![]() ;(2)M(-1,2);(3)满足条件的点P共有四个,分别为
;(2)M(-1,2);(3)满足条件的点P共有四个,分别为![]() (-1,-2),
(-1,-2), ![]() (-1,4),
(-1,4), ![]() (-1,
(-1,![]() ) ,
) ,![]() (-1,
(-1,![]() ).
).
【解析】
试题分析:(1)已知抛物线y=ax2+bx+c的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,可得方程组,解方程组可求得a、b、c的值,即可得抛物线的解析式;根据抛物线的对称性和点A的坐标(1,0)可求得B点的坐标(-3,0),用待定系数法可求得直线BC的解析式;(2)使MA+MC最小的点M应为直线BC与对称轴x=-1的交点,把x=-1代入直线BC的解析式求得y的值,即可得点M的坐标;(3)分①B为直角顶点,②C为直角顶点,③P为直角顶点三种情况分别求点P的坐标.
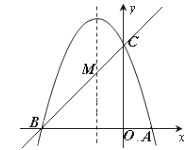
试题解析:(1)依题意,得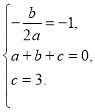 解之,得
解之,得
∴抛物线解析式为![]() .
.
∵对称轴为x=-1,且抛物线经过A(1,0),
∴B(-3,0).
把B(-3,0)、C(0,3)分别直线y=mx+n,得
![]() 解之,得
解之,得![]()
∴直线BC的解析式为![]() .
.
(2)∵MA=MB,∴MA+MC=MB+MC.
∴使MA+MC最小的点M应为直线BC与对称轴x=-1的交点.
设直线BC与对称轴x=-1的交点为M,把x=-1
代入直线![]() ,得y=2.
,得y=2.
∴M(-1,2)
(3)设P(-1,t),结合B(-3,0),C(0, 3),得BC2=18,
PB2=(-1+3)2+t2=4+t2,
PC2=(-1)2+(t-3)2=t2-6t+10.
①若B为直角顶点,则BC2+PB2=PC2,即18+4+t2=t2-6t+10.
解之,得t=-2.
②若C为直角顶点,则BC2+PC2=PB2,即
18+t2-6t+10=4+t2.解之,得t=4.
③若P为直角顶点,则PB2+PC2=BC2,即
4+t2+t2-6t+10=18.解之,得t1=![]() ,t2=
,t2=![]() .
.
综上所述,满足条件的点P共有四个,分别为![]() (-1,-2),
(-1,-2), ![]() (-1,4),
(-1,4), ![]() (-1,
(-1,![]() ) ,
) ,![]() (-1,
(-1,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD,AB=9,AD=4. E为CD边上一点,CE=6.
(1)求AE的长.
(2)点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE. 设点P运动的时间为t秒,则当t为何值时,△PAE为等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察探索:
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(x﹣1)(x4+x3+x2+x+1)=x5﹣1
根据规律填空:(x﹣1)(xn+xn﹣1+…+x+1)=__.(n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是七年级三班30名学生期末考试数学成绩表(已破损)

已知该班学生期末考试数学成绩平均分是76分.
(1)求该班80分和90分的人数分别是多少?
(2)设该班30名学生成绩的众数为a,中位数为b,求a+b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
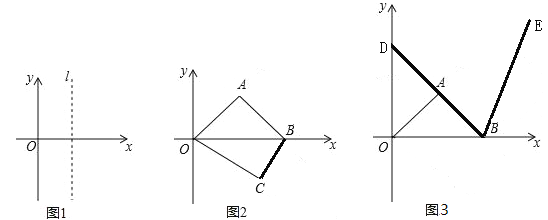
【题目】(1)观察与归纳:在如图1所示的平面直角坐标系中,直线l与y轴平行,点M与点N 是直线l上的两点(点M在点N的上方).
①亮亮发现:若点M坐标为(2,3),点N坐标为(2,﹣4),则MN的长度为_____; ②亮亮经过多次取l上的两点后,他归纳出这样的结论:若点M坐标为(t,m),点N坐标为(t,n),当m>n时,MN的长度可表示为______;
(2)如图2,四边形OABC的顶点O是坐标原点,点A在第一象限,![]() OAB=90
OAB=90![]() ,OA=AB,点C在第四象限,B点的坐标为(6,0),且OC=5.点P是线段OB上的一个动点(点P不与点0、B重合),过点P作与y轴平行的直线l,设点P横坐标为t.
,OA=AB,点C在第四象限,B点的坐标为(6,0),且OC=5.点P是线段OB上的一个动点(点P不与点0、B重合),过点P作与y轴平行的直线l,设点P横坐标为t.
①已知当t=4时,直线l恰好经过点C,求点A、C两点的坐标;
②在①的条件下,直线l上有一点M,当MB=![]() OC时,直接写出满足条件的点M坐标;
OC时,直接写出满足条件的点M坐标;
③如图3延长线段BA交y轴于点D将线段BD顺时针旋转60![]() ,D点的对应点为点E,是否存 在x轴上的点Q,使得QD+QE的值最小,若存在请求出点Q的坐标,并求出
,D点的对应点为点E,是否存 在x轴上的点Q,使得QD+QE的值最小,若存在请求出点Q的坐标,并求出![]() OQD的度数; 若不存在,请说明理由.
OQD的度数; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
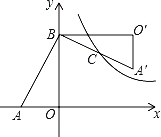
【题目】(2016湖北省荆州市第10题)如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数![]() 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
A.3 B.4 C.6 D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
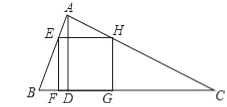
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com