
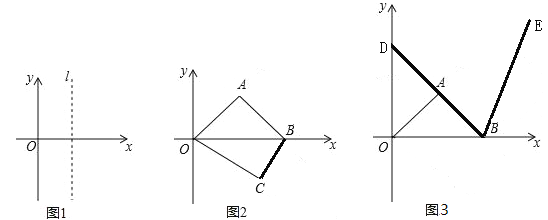
����Ŀ����1���۲�����ɣ�����ͼ1��ʾ��ƽ��ֱ������ϵ�У�ֱ��l��y��ƽ�У���M���N ��ֱ��l�ϵ����㣨��M�ڵ�N���Ϸ�����
���������֣�����M����Ϊ��2��3������N����Ϊ��2����4������MN�ij���Ϊ_____�� �������������ȡl�ϵ�����������ɳ������Ľ��ۣ�����M����Ϊ��t��m������N����Ϊ��t��n������m��nʱ��MN�ij��ȿɱ�ʾΪ______��
��2����ͼ2���ı���OABC�Ķ���O������ԭ�㣬��A�ڵ�һ���ޣ�![]() OAB=90
OAB=90![]() ��OA=AB����C�ڵ������ޣ�B�������Ϊ��6��0������OC=5����P���߶�OB�ϵ�һ�����㣨��P�����0��B�غϣ�������P����y��ƽ�е�ֱ��l�����P������Ϊt��
��OA=AB����C�ڵ������ޣ�B�������Ϊ��6��0������OC=5����P���߶�OB�ϵ�һ�����㣨��P�����0��B�غϣ�������P����y��ƽ�е�ֱ��l�����P������Ϊt��
����֪��t=4ʱ��ֱ��lǡ�þ�����C�����A��C��������ꣻ
���ڢٵ������£�ֱ��l����һ��M����MB=![]() OCʱ��ֱ��д�����������ĵ�M���ꣻ
OCʱ��ֱ��д�����������ĵ�M���ꣻ
����ͼ3�ӳ��߶�BA��y���ڵ�D���߶�BD˳ʱ����ת60![]() ��D��Ķ�Ӧ��Ϊ��E���Ƿ�� ��x���ϵĵ�Q,ʹ��QD+QE��ֵ��С���������������Q�����꣬�����
��D��Ķ�Ӧ��Ϊ��E���Ƿ�� ��x���ϵĵ�Q,ʹ��QD+QE��ֵ��С���������������Q�����꣬�����![]() OQD�Ķ����� �������ڣ���˵������.
OQD�Ķ����� �������ڣ���˵������.
���𰸡� ��1��7 m-n;(2)��A(3,3), C(4,-3),��M(4,![]() )��(4,-
)��(4,-![]() ); �۴��ڣ�Q(
); �۴��ڣ�Q(![]() ,0)��
,0)��![]() OQD=600
OQD=600
�������������������1��ֱ��l��y��ƽ�У�M��x1��y1����N��x2��y2����M��N�����������ȣ��ٸ���AB�ij���Ϊ|y1��y2|������ã�
(2) �ٹ�A����AE![]() OB�ڵ�E,��ֱ�����������߹�ϵ�ó���A��C�����ꣻ��ֱ�ӵó����ɣ�������QD��BF,����ֱ�������κͽ�ֱ��������
OB�ڵ�E,��ֱ�����������߹�ϵ�ó���A��C�����ꣻ��ֱ�ӵó����ɣ�������QD��BF,����ֱ�������κͽ�ֱ��������
�����������1���� 7 �� m-n
(2)��ͼ2. �ٹ�A����AE![]() OB�ڵ�E,
OB�ڵ�E,

![]()
![]() OAB=900,OA=AB ,B(6,0),AE
OAB=900,OA=AB ,B(6,0),AE![]() OB
OB
��OE=AE=BE=![]() OB=3,
OB=3, ![]() AOB=
AOB=![]() AOB= 450,A(3,3).
AOB= 450,A(3,3).
��Rt![]() OPC��OC=5,OP=4,��PC=3,
OPC��OC=5,OP=4,��PC=3,
��C(4,-3)
��M(4,![]() )��(4,-
)��(4,-![]() )
)
����ͼ3.��D�����x��ĶԳƵ�Ϊ��F,����EF��x���ڵ�Q,

����QD��BF,��![]() DBO=
DBO=![]() FBO=
FBO= ![]() BDO=
BDO=![]() BFO= 450,BD=BF,
BFO= 450,BD=BF,
OD=OB=6,![]() DBF=900.
DBF=900.
![]()
![]() DBE=600,BD=BE,
DBE=600,BD=BE,![]() DBF=900,
DBF=900,
��![]() FBE=1500,BE=BF,
FBE=1500,BE=BF,![]() BFE=150,
BFE=150,![]() QFO=300,
QFO=300,
�ɶԳƿ�֪��![]() QFO=
QFO=![]() QDO=300,��
QDO=300,��![]() OQD=600.
OQD=600.
��OQ=x,��DQ=2x
��Rt![]() ODQ��
ODQ�У�![]()
![]()
��![]()
��x=![]()
�� Q(![]() ,0)
,0)



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ��Rt�������߳��ֱ�Ϊ3��4��������߳���ƽ���ǣ� ����
A. 25 B. 14 C. 7 D. 7��25
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���E��F�ֱ���BC��CD�ϣ���AEF�ǵȱ������Σ�����AC��EF��G�����н��ۣ���BE=DF���ڡ�DAF=15�㣻��AC��ֱƽ��EF����BE+DF=EF����S��CEF=2S��ABE��������ȷ�����У�������

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
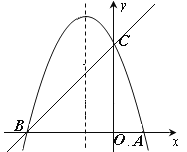
��ͼ����֪������y��ax2��bx��c(a��0)�ĶԳ���Ϊֱ��x����1���Ҿ���A��1��0����C��0��3�����㣬��x�����һ������ΪB.
����ֱ��y��mx��n����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
���������ߵĶԳ���x����1����һ��M��ʹ��M����A�ľ����뵽��C�ľ���֮����С�����M�����ꣻ�����PΪ�����ߵĶԳ���x����1�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016ɽ��ʡ�ij��е�22��)Ϊ�ӿ����Ⱥ�Ľ����뷢չ����A��B�����м��½����Ǽ���·�����ɺ���·������������ڵ�120km������114km���Ǽ���·�����ƽ��ʱ��Ҫ�����е�ƽ��ʱ�ٿ�110km������ʱ���������ʱ���![]() ���ɺ�ijǼ���·��A��B���ص�����ʱ�䣮
���ɺ�ijǼ���·��A��B���ص�����ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼף������������ڴ��и�װ��10����3����״��С��ȫ��ͬ�ĺ�ɫС�������������ɫС��ĸ�����P��_____P�������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016����ʡ�����е�9��)��ͼ�����߶�AB�Ƶ�O˳ʱ����ת90���õ��߶�A��B������ôA����2��5���Ķ�Ӧ��A���������ǣ� ��
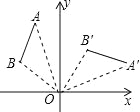
A����2��5�� B����5��2�� C����2����5�� D����5����2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
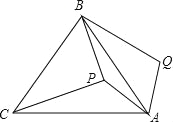
����Ŀ����ͼ��P�ǵȱ�������ABC��һ�㣬���߶�AP�Ƶ�A˳ʱ����ת60��õ��߶�AQ������BQ����PA=6��PB=8��PC=10�����ı���APBQ�����Ϊ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com