Question

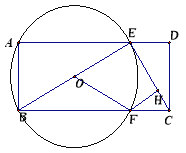
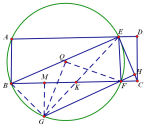
【题目】已知矩形ABCD中，AB＝2，AD＝5，点E是AD边上一动点，连接BE、CE，以BE为直径作⊙O，交BC于点F，过点F作FH⊥CE于H．

（Ⅰ）当直线FH与⊙O相切时，求AE的长；

（Ⅱ）若直线FH交⊙O于点G，

（ⅰ）当FH∥BE时，求的长；

（ⅱ）在点E运动过程中，△OFG能否成为等腰直角三角形？如果能，求出此时AE的长；如果不能，说明理由．

Answer 1

【答案】（Ⅰ）AE =2.5（Ⅱ）（ⅰ）1或4（ⅱ） 或

【解析】

试题分析：（Ⅰ）连接OF，EF， 利用切线的性质、三角形中位线定理证明点F是BC中点，四边形ABFE是矩形, 从而可得BF=AE =2.5；（Ⅱ）（ⅰ）根据FH∥BE得出ΔAEB∽ΔEDC，然后利用相似三角形的对应边成比例可求出AE的长；（ⅱ）分①当G在点F的上方时和当G在点F的下方时两种情况讨论，①当G在点F的上方时，可确定AE=，当G在点F的下方时，可确定.

试题解析：（Ⅰ）连接OF，EF，

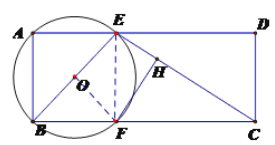
∵FH为切线，点F为切点，

∴OFFH

又∵FH⊥CE ∴OF∥CE

∵O为BE中点 ∴点F是BC中点

又AD=BC=5，所以BF=2.5

∵矩形ABCD中，BE为直径 BFE=90

∴A=B=BFE=90

∴ABFE也是矩形, BF=AE =2.5

（Ⅱ）（ⅰ）∵FH∥BE FH⊥CE ∴BEC=90

可证△AEB∽△EDC

设AE=x， 则AE：QB=CD：DE 所以x：2=2：（5-x）

解得x=1或4

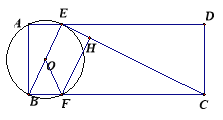
（ⅱ）①当G在点F的上方时

连接EF，OG，OF，BG，EF与BG交点为K，作GM⊥EF于M

设AE=x，EF=AB=2，BF=AE=x，∴∠FOG=90 在圆O中∠FBK=∠GEK=45°

可证明BFk和EGK为等腰直角三角形

设FM=BF=x ，则EK=2-x

GM=KM=，

可证：GFM∽EFC

所以， ，

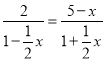得

∴AE=

②当G在点F的下方时

连BG，EG，EF，OE，OF，作GM⊥BF

同理可证BGK，EFK为等腰直角三角形，

设AE=x，EF=AB=2，BF=AE=x，

∵FOG=90 ， KF=EF=2， ，，

∴ ，

可证GFM∽ECF

∴ ，即：

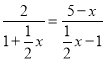
（舍去负值），即

综上： 或