
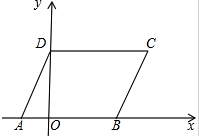
 如图所示,平行四边形ABCD中,顶点A,B,D在坐标轴上,AD=5,AB=9,点A的坐标为(-3,0),则点C的坐标为( )
如图所示,平行四边形ABCD中,顶点A,B,D在坐标轴上,AD=5,AB=9,点A的坐标为(-3,0),则点C的坐标为( )| A. | (6,5) | B. | (9,4) | C. | (6,4) | D. | (9,5) |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | -9的立方根是-3 | B. | ±7是49的平方根 | ||
| C. | 有理数与数轴上的点一一对应 | D. | $\sqrt{81}$算术平方根是9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,M,N分别是线段BC,AB上的动点,(含端点,但点M不与点B重合),E,F分别为DM,MN的中点,则EF长度的最大值为( )
如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,M,N分别是线段BC,AB上的动点,(含端点,但点M不与点B重合),E,F分别为DM,MN的中点,则EF长度的最大值为( )| A. | 4 | B. | 3 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$=±3 | B. | $\root{3}{-8}$=2 | C. | ±$\sqrt{9}$=3 | D. | ${(\root{3}{-8})}^{2}$=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 消费卡 | 消费方式 |
| 普通卡 | 35元/次 |
| 白金卡 | 280元/张,凭卡免费消费10次再送2次 |
| 钻石卡 | 560元/张,凭卡每次消费不再收费 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为8的正方形ABCD中,E是AB上的点,⊙O是以BC为直径的圆.
如图,在边长为8的正方形ABCD中,E是AB上的点,⊙O是以BC为直径的圆.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com