
【题目】如图,△ABC中,∠C=90°,AC=BC,点D是AB的中点,分别过点D作DE⊥AC,DF⊥BC,垂足分别为点E、F.求证:四边形CEDF是正方形.
【答案】证明:连接CD.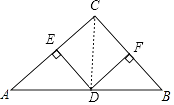
∵DE⊥AC,DF⊥BC,
∠CED=90°,∠CFD=90°,
∵∠C=90°,
∴四边形CEDF是矩形,
∵AC=BC,D是AB中点,
∴DC平分∠ACB,
∵DE⊥AC,DF⊥CB,
∴DE=DF,
∴四边形CEDF是正方形.
【解析】连接CD,先根据三个角是直角的四边形是矩形,证明四边形CEDF是矩形,再根据已知证明DE=DF,即可证得结论。
【考点精析】本题主要考查了线段的中点和角平分线的性质定理的相关知识点,需要掌握线段的中点到两端点的距离相等;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能正确解答此题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.
(1)求证:BP=EP;
(2)若CE=3,BE=6,求∠CPE的度数;
(3)探究AP、PC、BE之间的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE上一定点(其中EP<PD)
(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.
①求证:PG=PF; ②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.
(2)拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA于点G,你认为(1)中DF、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小方与同学一起去郊游,看到一棵大树斜靠在一小土坡上,他想知道树有多长,于是他借来测角仪和卷尺.如图,他在点C处测得树AB顶端A的仰角为30°,沿着CB方向向大树行进10米到达点D,测得树AB顶端A的仰角为45°,又测得树AB倾斜角∠1=75°.
(1)求AD的长.
(2)求树长AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有![]() 个,若从中随机摸出一个球,这个球是白球的概率为
个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(![]() )请直接写出袋子中白球的个数.
)请直接写出袋子中白球的个数.
(![]() )随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列选项中,可以用来说明命题“两个锐角的和是锐角”是假命题的反例的是( )
A.∠A=30°,∠B=40°
B.∠A=30°,∠B=110°
C.∠A=30°,∠B=70°
D.∠A=30°,∠B=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com