
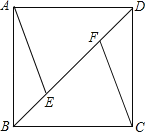
【题目】平面内有一等腰直角三角板(∠ACB=90°)和一直线MN,过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.当点E与点A重合时(如图①),易证:AF+BF=2CE;当三角板绕点A顺时针旋转至图②、图③的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,请直接写出你的猜想,不需证明.

【答案】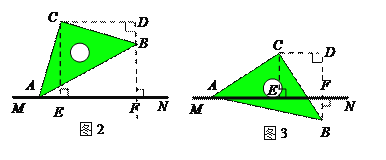
图2成立
过点C作CD⊥BF,交FB的延长线于点D
证出△AEC≌△BDC,∴CE=CD,AE=BD
证出四边形CEFD是正方形,∴CE=EF=DF
∴AF+BF=AE+EF+DF-BD,AF+BF=2CE
图3不成立
应为AF-BF=2CE
【解析】
过B作BH⊥CE与点H,易证△ACE≌△CBH,根据全等三角形的对应边相等,即可证得AF+BF=2CE.
图2,AF+BF=2CE仍成立,
证明:过B作BH⊥CE于点H,
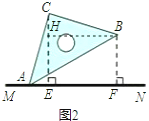
∵∠BCH+∠ACE=90°,
又∵在直角△ACE中,∠ACE+∠CAE=90°,
∴∠CAE=∠BCH,
又∵AC=BC,∠AEC=∠BHC=90°
∴△ACE≌△CBH.
∴CH=AE,BF=HE,CE=BH,
∴AF+BF=AE+EF+BF=CH+EF+HE=CE+EF=2EC.
图3中,过点C作CG⊥BF,交BF延长线于点G,
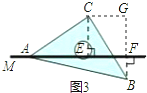
∵AC=BC,
可得∠AEC=∠CGB,
∠ACE=∠BCG,
∴△CBG≌△CAE,
∴AE=BG,
∵AF=AE+EF,
∴AF=BG+CE=BF+FG+CE=2CE+BF,
∴AF-BF=2CE.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的大小;
(2)若CD=3,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
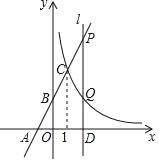
【题目】如图,直线y=kx+2与x轴,y轴分别交于点A(﹣1,0)和点B,与反比例函数y=![]() 的图象在第一象限内交于点C(1,n).
的图象在第一象限内交于点C(1,n).
(1)求一次函数y=kx+2与反比例函数y=![]() 的表达式;
的表达式;
(2)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线y=kx+2和双曲线y=![]() 交于P、Q两点,且PQ=2QD,求点D的坐标.
交于P、Q两点,且PQ=2QD,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,AB=4,点E,F在对角线BD上,AE∥CF.
(1)求证:△ABE≌△CDF;
(2)若∠ABE=2∠BAE,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC的边AB,AC的外侧分别作等边△ABD和等边△ACE,连接DC,BE.
(1)求证:DC=BE;
(2)若BD=3,BC=4, BD⊥BC于点B,请求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
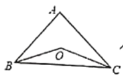
【题目】(1)如图所示,已知![]() 中,
中,![]() 的平分线相交于点
的平分线相交于点![]() ,试猜想
,试猜想![]() 与
与![]() 的关系,并证明.
的关系,并证明.
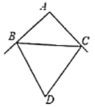
(2)如图所示,在![]() 中,
中,![]() 分别是
分别是![]() 的外角平分线,试猜想
的外角平分线,试猜想![]() 与
与![]() 的关系_____ (直接写结果不要证明)
的关系_____ (直接写结果不要证明)
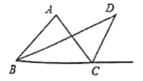
(3)如图所示,已知![]() 为
为![]() 的角平分线,
的角平分线,![]() 为
为![]() 外角
外角![]() 的平分线,且与
的平分线,且与![]() 交于点
交于点![]() ,试猜想
,试猜想![]() 与
与![]() 的关系_____ (直接写结果不要证明)
的关系_____ (直接写结果不要证明)
(1) (2)
(2)  (3)
(3) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有三个小球,小球上分别标有数字-2、l、2,它们除了数字不同外,其它都完全相同.
(1)随机地从布袋中摸出一个小球,则摸出的球为标有数字l的小球的概率为 .
(2)小红先从布袋中随机摸出一个小球,记下数字作为![]() 的值,再把此球放回袋中搅匀,由小亮从布袋中随机摸出一个小球,记下数字作为
的值,再把此球放回袋中搅匀,由小亮从布袋中随机摸出一个小球,记下数字作为![]() 的值,请用树状图或表格列出
的值,请用树状图或表格列出![]() 、
、![]() 的所有可能的值,并求出直线
的所有可能的值,并求出直线![]() 不经过第四象限的概率.
不经过第四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一,下列图表中的数据是运动员甲、乙、丙三人每人10次垫球测试的成绩,测试规则为每次连续接球10个,每垫球到位1个记1分,已知运动员甲测试成绩的中位数和众数都是7.
运动员甲测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 |
| 6 | 8 | 6 | 8 |
|
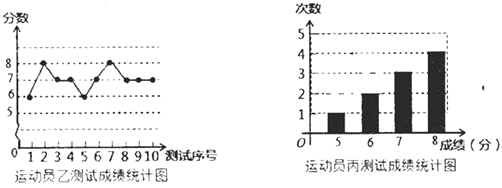
(1)填空:![]() ______;
______;![]() ______.
______.
(2)要从他们三人中选择一位垫球较为稳定的接球能手,你认为选谁更合适?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.


(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com