
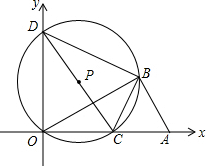
 如图,在平面直角坐标系中,Rt△ABO的斜边OA在x轴上,点B在第一象限内,AO=4,∠BOA=30°.点C(t,0)是x轴正半轴上一动点(不与O,A重合),△OBC的外接圆⊙P与y轴的另一交点为D.
如图,在平面直角坐标系中,Rt△ABO的斜边OA在x轴上,点B在第一象限内,AO=4,∠BOA=30°.点C(t,0)是x轴正半轴上一动点(不与O,A重合),△OBC的外接圆⊙P与y轴的另一交点为D.分析 (1)过点B作BH⊥OA于H,如图1,在Rt△OBA中运用三角函数可求出AB,OB,在Rt△OHB中运用三角函数可求出OH,BH,就可得到点B的坐标;
(2)在Rt△OCD中,OC=t,要求OD,只需求出DC,易得DC=2BC,只需求出BC,在Rt△BHC中运用勾股定理即可解决问题;
(3)可分点Q在直线OB的上方和下方两种情况讨论:①若Q在直线OB的下方,易证当点Q在点A处时满足要求,显然过点A平行于OB的直线与抛物线的另一个交点也满足要求,只需求出该直线的解析式,然后求出该直线与抛物线的交点坐标,就可解决问题;②若Q在直线OB的上方,易得过点Q平行于OB的直线的解析式,只需求出该直线与抛物线的交点坐标,就可解决问题.
解答 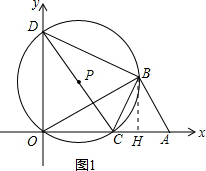 解:(1)过点B作BH⊥OA于H,如图1,
解:(1)过点B作BH⊥OA于H,如图1,
∵∠ABO=90°,AO=4,∠BOA=30°,
∴AB=OA•sin∠AOB=4×$\frac{1}{2}$=2,
OB=OA•cos∠AOB=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$.
∴BH=OB•sin∠HOB=2$\sqrt{3}$×$\frac{1}{2}$=$\sqrt{3}$,
OH=OB•cos∠HOB=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,
∴B(3,$\sqrt{3}$);
(2)在Rt△BHC中,
BC=$\sqrt{C{H}^{2}+B{H}^{2}}$=$\sqrt{(3-t)^{2}+(\sqrt{3})^{2}}$=$\sqrt{{t}^{2}-6t+12}$.
∵∠COD=90°,
∴CD是⊙P的直径,
∴∠CBD=90°.
∵∠BDC=∠BOC=30°,
∴BC=DC•sin∠BDC=$\frac{1}{2}$DC,
∴DC=2BC=2$\sqrt{{t}^{2}-6t+12}$,
∴OD2=CD2-OC2=4(t2-6t+12)-t2=3t2-24t+48,
∴OD=$\sqrt{3{t}^{2}-24t+48}$;
(3)①若点Q在OB下方,
∵AB=2,∠ABO=90°,
∴当点Q在点A处,以Q为圆心,2为半径的圆与直线OB相切,
此时点Q的坐标为(4,0).
过点A作OB的平行线,交y轴于点E,如图2,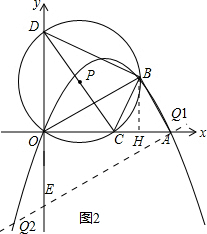
则有∠OAE=∠BOA=30°,
∴OE=OA•tan∠OAE=4×$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
∴E(0,-$\frac{4\sqrt{3}}{3}$).
设直线AE的解析式为y=kx+b,
则有$\left\{\begin{array}{l}{4k+b=0}\\{b=-\frac{4\sqrt{3}}{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=-\frac{4\sqrt{3}}{3}}\end{array}\right.$,
直线AE的解析式为y=$\frac{\sqrt{3}}{3}$x-$\frac{4\sqrt{3}}{3}$.
设过点O(0,0),A(4,0),B(3,$\sqrt{3}$)的抛物线解析式为
y=ax(x-4),
则有$\sqrt{3}$=a×3×(3-4),
解得a=-$\frac{\sqrt{3}}{3}$,
∴抛物线解析式为y=-$\frac{\sqrt{3}}{3}$x(x-4).
解$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x-\frac{4\sqrt{3}}{3}}\\{y=-\frac{\sqrt{3}}{3}x(x-4)}\end{array}\right.$得
$\left\{\begin{array}{l}{x=-1}\\{y=-\frac{5\sqrt{3}}{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=0}\end{array}\right.$,
∴点Q的坐标为(-1,-$\frac{5\sqrt{3}}{3}$)或(4,0).
②若点Q在OB上方,
则过点Q平行于OB的直线的解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$,
联立$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x+\frac{4\sqrt{3}}{3}}\\{y=-\frac{\sqrt{3}}{3}x(x-4)}\end{array}\right.$,
该方程组无解,
综上所述:点Q的坐标为(-1,-$\frac{5\sqrt{3}}{3}$)或(4,0).
点评 本题主要考查了运用待定系数法求直线及抛物线的解析式、直线与抛物线的交点坐标、解方程组、勾股定理、三角函数的定义、圆周角定理、切线的判定等知识,综合性比较强,需要注意的是由于点Q相对于OB的位置不确定,因此需分情况讨论.


科目:初中数学 来源: 题型:解答题
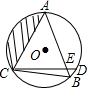 如图,在⊙O中,$\widehat{AD}$=$\widehat{AC}$,弦CD与弦AB交于点E,连接BC,若⊙O的半径长为4cm,∠ACD=60°,求图中阴影部分的面积.
如图,在⊙O中,$\widehat{AD}$=$\widehat{AC}$,弦CD与弦AB交于点E,连接BC,若⊙O的半径长为4cm,∠ACD=60°,求图中阴影部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$x${\;}^{{n}^{2}}$-2xnm+1 | B. | $\frac{1}{3}$x${\;}^{{n}^{2}}$-$\frac{1}{3}$xnm+$\frac{2}{3}$xn | ||
| C. | $\frac{1}{3}$x2n-$\frac{4}{3}$xm+n+$\frac{2}{3}$xn | D. | $\frac{1}{3}$x2n-$\frac{4}{3}$xm+n+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com