
【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于A、B两点,其中点A的横坐标是-2.
交于A、B两点,其中点A的横坐标是-2.
⑴求这条直线的函数关系式及点B的坐标 ;
⑵在![]() 轴上是否存在点C,使得ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在点C,使得ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
⑶.过线段AB上一点P,作PM∥![]() 轴,交抛物线于点M,点M在第一象限;点
轴,交抛物线于点M,点M在第一象限;点![]() ,当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
,当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?

【答案】(1)点B的坐标为(8,16);(2)点C的坐标为(![]() ,0),(0,0),(6,0),(32,0);(3)当M的横坐标为6时,MN+3PM的长度的最大值是18.
,0),(0,0),(6,0),(32,0);(3)当M的横坐标为6时,MN+3PM的长度的最大值是18.
【解析】试题分析:(1)、根据点A在二次函数上求出点A的坐标,然后利用待定系数法求出一次函数的解析式,根据一次函数和二次函数的交点坐标求出求出点B的坐标;(2)、根据点A和点B的坐标求出![]() 的值,设点C的坐标为(m,0),然后分别求出
的值,设点C的坐标为(m,0),然后分别求出![]() 和
和![]() 的值,然后根据勾股定理分三种情况进行讨论,分别求出m的值,得出点C的坐标;(3)、设点M的坐标为:(a,
的值,然后根据勾股定理分三种情况进行讨论,分别求出m的值,得出点C的坐标;(3)、设点M的坐标为:(a, ![]() ),MP与y轴交于点Q,根据Rt△MQN的勾股定理求出MN的长度,根据点P和点M的纵坐标相等得出点P的横坐标为
),MP与y轴交于点Q,根据Rt△MQN的勾股定理求出MN的长度,根据点P和点M的纵坐标相等得出点P的横坐标为![]() ,从而得出MN+3MP关于a的函数解析式,然后利用二次函数的性质得出最大值.
,从而得出MN+3MP关于a的函数解析式,然后利用二次函数的性质得出最大值.
试题解析:(1)、∵点A是直线与抛物线的交点,且横坐标为﹣2,
∴y=![]() ×(﹣2)2=1,A点的坐标为(﹣2,1),
×(﹣2)2=1,A点的坐标为(﹣2,1),
设直线的函数关系式为y=kx+b,
将(0,4),(﹣2,1)代入得: ![]() ,解得:
,解得: 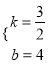 ,
,
∴直线y=![]() x+4, ∵直线与抛物线相交, ∴
x+4, ∵直线与抛物线相交, ∴![]() x+4=
x+4=![]() x2,解得:x=﹣2或x=8,
x2,解得:x=﹣2或x=8,
当x=8时,y=16, ∴点B的坐标为(8,16);
(2)、如图1,连接AC,BC, ∵由A(﹣2,1),B(8,16)可求得AB2=325.
设点C(m,0),同理可得AC2=(m+2)2+12=m2+4m+5, BC2=(m﹣8)2+162=m2﹣16m+320,
①若∠BAC=90°,则AB2+AC2=BC2,即325+m2+4m+5=m2﹣16m+320,解得:m=﹣![]() ;
;
②若∠ACB=90°,则AB2=AC2+BC2,即325=m2+4m+5+m2﹣16m+320, 解得:m=0或m=6;
③若∠ABC=90°,则AB2+BC2=AC2,即m2+4m+5=m2﹣16m+320+325, 解得:m=32;
∴点C的坐标为(﹣![]() ,0),(0,0),(6,0),(32,0)
,0),(0,0),(6,0),(32,0)
(3)设M(a, ![]() ),设MP与y轴交于点Q,
),设MP与y轴交于点Q,
在Rt△MQN中,由勾股定理得MN=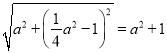 ,
,
又∵点P与点M纵坐标相同, ∴![]() +4=
+4=![]() , ∴x=
, ∴x=![]() , ∴点P的横坐标为
, ∴点P的横坐标为![]() ,
,
∴MP=a﹣![]() , ∴MN+3PM=
, ∴MN+3PM=![]() +1+3(a﹣
+1+3(a﹣![]() )=﹣
)=﹣![]() +3a+9,
+3a+9,

∴当a=﹣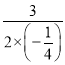 =6, 又∵﹣2≤6≤8, ∴取到最大值18,
=6, 又∵﹣2≤6≤8, ∴取到最大值18,
∴当M的横坐标为6时,MN+3PM的长度的最大值是18.


科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为![]() .其中正确的结论有( )
.其中正确的结论有( )
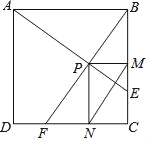
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的三个顶点的坐标分别为A(-3,2)、B(0,4)、C(0,2).
⑴将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C.平移△ABC,若A对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
⑵若将△A1B1C绕某一点旋转得到△A2B2C2,请直接写出旋转中心的坐标为 .
⑶在x轴上找一点P,使得直线CP将△ABC的面积分为1:2,直接写出P点的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AC与BD交于点E,点E是BD的中点,延长CD到点F,使DF=CD,连接AF,
(1)求证:AE=CE;
(2)求证:四边形ABDF是平行四边形;
(3)若AB=2,AF=4,∠F=30°,则四边形ABCF的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青海新闻网讯:2016年2月21日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了112万元,建成40个公共自行车站点、配置720辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2018年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
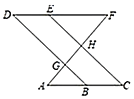
【题目】如图,点![]() ,
,![]() 分别在直线
分别在直线![]() 和
和![]() 上,若
上,若![]() ,
,![]() ,可以证明
,可以证明![]() .请完成下面证明过程中的各项“填空”.
.请完成下面证明过程中的各项“填空”.
证明:∵![]() (理由:______.)
(理由:______.)
![]() ______(对顶角相等)
______(对顶角相等)
∴![]() ,∴
,∴![]() (理由:______)
(理由:______)
∴![]() ______
______![]() (两直线平行,同位角相等)
(两直线平行,同位角相等)
又∵![]() ,∴
,∴![]() ,
,
∴![]() ______(内错角相等,两直线平行)
______(内错角相等,两直线平行)
∴![]() (理由:______)
(理由:______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).


请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了_____名学生.
(2)补全条形统计图中的缺项.
(3)在扇形统计图中,选择教师传授的占_____%,选择小组合作学习的占_____%.
(4)根据调查结果,估算该校1800名学生中大约有_____人选择小组合作学习模式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为( ).(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)

A.164m B.178m C.200m D.1618m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生校园生活,满足学生的多元文化需求,促进学生身心健康和谐发展,学校开展了丰富多彩的社团活动.我区某中学开展的社团活动有:A.尤克里里、B.街舞、C.羽毛球、D.口琴、E.沙画.学生管理中心为了了解全校800名学生的社团需求,开展了一次调查研究,请将下面的调查过程补全.
抽样调查:学生管理中心计划选取40名学生进行问卷调查,下面的抽样方法中, 合理的是 (填序号);
①从七、八、九三个年级中随机抽取40名女生进行问卷调查;
②从七、八、九三个年级中随机抽取男、女生共40名进行问卷调查.
收集数据:抽样方法确定后,学生管理中心收集到如下数据(社团项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B
A,C,E,D,B,A,B,E,C,A
D,D,B,B,C,C,A,A,E,B
C,B,D,C,A,C,C,A,C,E
整理、描述数据:划记、整理、描述样本数据、绘制统计图如下,请补全统计表和统计图.
选择各社团项目的人数统计表
社团项目 | 划记 | 人数 |
A尤克里里 | 正 | 8 |
B街舞 | ||
C羽毛球 | 正正丅 | 12 |
D口琴 | ||
E沙画 | 正一 | 6 |
合计 | 40 | 40 |

分析数据、推断结论:
(1)在扇形统计图中,“B街舞”所在的扇形的圆心角等于 度;
(2)根据学生管理中心获得的样本数据估计全校大约有多少名同学选择羽毛球这个社团?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com