
【题目】如图,点![]() ,
,![]() 分别在直线
分别在直线![]() 和
和![]() 上,若
上,若![]() ,
,![]() ,可以证明
,可以证明![]() .请完成下面证明过程中的各项“填空”.
.请完成下面证明过程中的各项“填空”.
证明:∵![]() (理由:______.)
(理由:______.)
![]() ______(对顶角相等)
______(对顶角相等)
∴![]() ,∴
,∴![]() (理由:______)
(理由:______)
∴![]() ______
______![]() (两直线平行,同位角相等)
(两直线平行,同位角相等)
又∵![]() ,∴
,∴![]() ,
,
∴![]() ______(内错角相等,两直线平行)
______(内错角相等,两直线平行)
∴![]() (理由:______)
(理由:______)
【答案】见解析.
【解析】
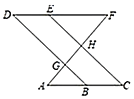
根据对顶角相等推知同位角∠EHF=∠DGF,从而证得两直线DB∥EC;然后由平行线的性质及已知得到内错角∠DBA=∠D,即可根据平行线的判定定理推知两直线DF∥AC;最后由平行线的性质(两直线平行,内错角相等)证得∠A=∠F.
解:∵∠AGB=∠EHF(理由:已知),∠AGB=∠DGF(对顶角相等),
∴∠EHF=∠DGF,
∴DB∥EC(理由:同位角相等,两直线平行),
∴∠C=∠DBA ( 两直线平行,同位角相等),
又∵∠C=∠D(已知),
∴∠DBA=∠D(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(理由:两直线平行,内错角相等).
故答案为:已知;∠DGF;同位角相等,两直线平行;C;AC;两直线平行,内错角相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于A、B两点,其中点A的横坐标是-2.
交于A、B两点,其中点A的横坐标是-2.
⑴求这条直线的函数关系式及点B的坐标 ;
⑵在![]() 轴上是否存在点C,使得ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在点C,使得ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
⑶.过线段AB上一点P,作PM∥![]() 轴,交抛物线于点M,点M在第一象限;点
轴,交抛物线于点M,点M在第一象限;点![]() ,当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
,当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
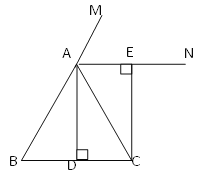
【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司组织退休职工组团前往某景点游览参观,参加人员共70人.旅游景点规定:①门票每人60元,无优惠;②上山游览必须乘坐景点安排的观光车游览,观光车有小型车和中型车两类,分别可供4名和11名乘客乘坐;且小型车每辆收费60元,中型车每人收费10元.若70人正好坐满每辆车且参观游览的总费用不超过5000元,问景点安排的小型车和中型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
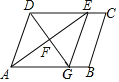
【题目】如图,四边形ABCD是平行四边形,AE平分∠BAD交CD于点E,AE的垂直平分线交AB于点G,交AE于点F.若AD=4cm,BG=1cm,则AB=_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究如图,直线![]() 的解析式为
的解析式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() 和点
和点![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() .
.
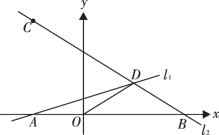
(1)求直线![]() 的解析式;
的解析式;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)求![]() 的面积;
的面积;
(4)探究在直线![]() 上是否存在异于点
上是否存在异于点![]() 的另一点
的另一点![]() ,使得
,使得![]() 与
与![]() 的面积相等,若存在,请直接写出点
的面积相等,若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com