
分析 (1)根据零指数幂的意义、特殊角的锐角三角函数以及负整数指数幂的意义即可求出答案;
(2)先化简原式,然后将a的值代入即可求出答案.
解答 解:(1)原式=3+1-(-2)2-2×$\frac{1}{2}$=4-4-1=-1
(2)当a=-2+$\sqrt{2}$
原式=$\frac{2}{(a-1)(a+1)}$+$\frac{4+2a}{(a+1)(a-1)}$
=$\frac{6+2a}{{a}^{2}-1}$
=$\frac{2+2\sqrt{2}}{5-4\sqrt{2}}$
=$-\frac{26+18\sqrt{2}}{7}$
点评 本题考查学生的运算能力,解题的关键是熟练运用运算法则,本题属于基础题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
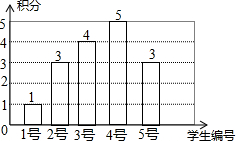 编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记0分,如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.
编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记0分,如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
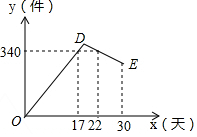 某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF∥AB,与过点B的切线交于点F,连接BD.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF∥AB,与过点B的切线交于点F,连接BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com