
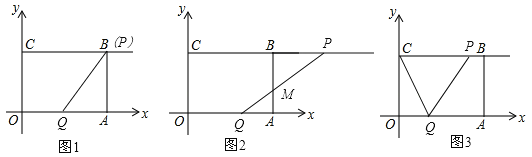
【题目】已知:如图所示,在平面直角坐标系xoy中,四边形OABC是矩形,OA=4,OC=3,动点P从点C出发,沿射线CB方向以每秒2个单位长度的速度运动;同时,动点Q从点O出发,沿x轴正半轴方向以每秒1个单位长度的速度运动.设点P、点Q的运动时间为t(s).
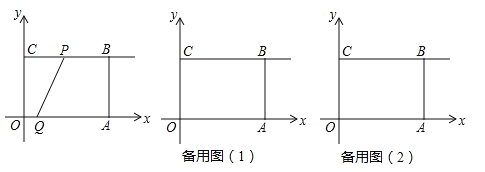
(1)当t=1s时,求经过点O,P,A三点的抛物线的解析式;
(2)当t=2s时,求tan∠QPA的值;
(3)当线段PQ与线段AB相交于点M,且BM=2AM时,求t(s)的值;
(4)连接CQ,当点P,Q在运动过程中,记△CQP与矩形OABC重叠部分的面积为S,求S与t的函数关系式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)t=3s;(4)
;(3)t=3s;(4) .
.
【解析】
(1)可求得P点坐标,由O、P、A的坐标,利用待定系数法可求得抛物线解析式;
(2)当t=2s时,可知P与点B重合,在Rt△ABQ中可求得tan∠QPA的值;
(3)用t可表示出BP和AQ的长,由△PBM∽△QAM可得到关于t的方程,可求得t的值;
(4)当点Q在线段OA上时,S=S△CPQ;当点Q在线段OA上,且点P在线段CB的延长线上时,由相似三角形的性质可用t表示出AM的长,由S=S四边形BCQM=S矩形OABC﹣S△COQ﹣S△AMQ,可求得S与t的关系式;当点Q在OA的延长线上时,设CQ交AB于点M,利用△AQM∽△BCM可用t表示出AM,从而可表示出BM,S=S△CBM,可求得答案.
(1)当t=1s时,则CP=2,∵OC=3,四边形OABC是矩形,∴P(2,3),且A(4,0),
∵抛物线过原点O,∴可设抛物线解析式为![]() ,
,
∴![]() ,解得:
,解得: ,
,
∴过O、P、A三点的抛物线的解析式为![]() ;
;
(2)当t=2s时,则CP=2×2=4=BC,即点P与点B重合,OQ=2,如图1,
∴AQ=OA﹣OQ=4﹣2=2,且AP=OC=3,
∴tan∠QPA=![]() =
=![]() ;
;
(3)当线段PQ与线段AB相交于点M,则可知点Q在线段OA上,点P在线段CB的延长线上,如图2,
则CP=2t,OQ=t,∴BP=PC﹣CB=2t﹣4,AQ=OA﹣OQ=4﹣t,
∵PC∥OA,∴△PBM∽△QAM,
∴![]() ,且BM=2AM,
,且BM=2AM,
∴![]() =2,解得t=3,
=2,解得t=3,
∴当线段PQ与线段AB相交于点M,且BM=2AM时,t为3s;
(4)当0≤t≤2时,如图3,由题意可知CP=2t,∴S=S△PCQ=![]() ×2t×3=3t;
×2t×3=3t;
当2<t≤4时,设PQ交AB于点M,
如图4,由题意可知PC=2t,OQ=t,则BP=2t﹣4,AQ=4﹣t,
同(3)可得![]() =
=![]() ,
,
∴BM=![]() AM,∴3﹣AM=
AM,∴3﹣AM=![]() AM,解得AM=
AM,解得AM=![]() ,
,
∴S=S四边形BCQM=S矩形OABC﹣S△COQ﹣S△AMQ=3×4﹣![]() ×t×3﹣
×t×3﹣![]() ×(4﹣t)×
×(4﹣t)×![]() =24﹣
=24﹣![]() ﹣3t;
﹣3t;
当t>4时,设CQ与AB交于点M,如图5,由题意可知OQ=t,AQ=t﹣4,
∵AB∥OC,∴![]() ,即
,即![]() ,解得AM=
,解得AM=![]() ,
,
∴BM=3﹣![]() =
=![]() ,∴S=S△BCM=
,∴S=S△BCM=![]() ×4×
×4×![]() =
=![]() ;
;
综上可知: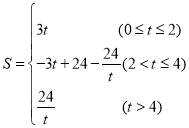 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
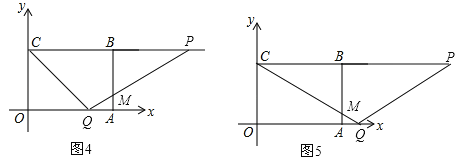
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
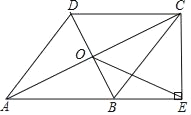
【题目】已知点A,B分别在x轴和y轴上,且![]() ,点C的坐标是
,点C的坐标是![]() ,AB与OC相交于点G.点P从O出发以每秒1个单位的速度从O运动到C,过P作直线
,AB与OC相交于点G.点P从O出发以每秒1个单位的速度从O运动到C,过P作直线![]() 分别交OA,OB或AC,BC于E,F.解答下列问题:
分别交OA,OB或AC,BC于E,F.解答下列问题:
(1)直接写出点G的坐标;
(2)若点P运动的时间为t,直线EF在四边形OACB内扫过的面积为s,请求出s与t的函数关系式;并求出当t为何值时,直线EF平分四边形OACB的面积;
(3)设线段OC的中点为Q,P运动的时间为t,求当t为何值时,![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
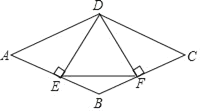
【题目】如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DE⊥BC于点F,连接EF,求证:
(1)△ADE≌△CDF;
(2)若∠A=60°,AD=4,求△EDF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有黄球、黑球和红球共40个,它们除颜色外都相同,其中红球有22个,且经过试验发现摸出一个球为黄球的频率接近0.125 。
⑴求袋中有多少个黑球;
⑵现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个球是黄球的概率达到![]() ,问至少取出了多少个黑球?
,问至少取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,O为坐标原点,横、纵轴的单位长度相同,A、B的坐标分别为(8,6),(16,0),点P沿OA边从点O开始向终点A运动,速度每秒1个单位,点Q沿BO边从B点开始向终点O运动,速度每秒2个单位,如果P、Q同时出发,用t(秒)表示移动时间,当这两点中有一点到达自己的终点时,另一点也停止运动。求:

(1)几秒时PQ∥AB.
(2)设△OPQ的面积为y,求y与t的函数关系式.
(3)△OPQ与△OAB能否相似?若能,求出点P的坐标,若不能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
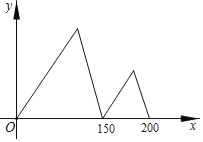
【题目】甲、乙两人在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑步1000米,甲超出乙150米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与乙出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙距离终点还有_____米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com