
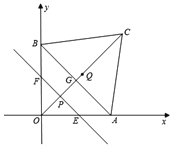
����Ŀ����֪��A��B�ֱ���x���y���ϣ���![]() ����C��������
����C��������![]() ��AB��OC�ཻ�ڵ�G����P��O������ÿ��1����λ���ٶȴ�O�˶���C����P��ֱ��
��AB��OC�ཻ�ڵ�G����P��O������ÿ��1����λ���ٶȴ�O�˶���C����P��ֱ��![]() �ֱ�OA��OB��AC��BC��E��F������������⣺
�ֱ�OA��OB��AC��BC��E��F������������⣺
��1��ֱ��д����G�����ꣻ
��2������P�˶���ʱ��Ϊt��ֱ��EF���ı���OACB��ɨ�������Ϊs�������s��t�ĺ�����ϵʽ���������tΪ��ֵʱ��ֱ��EFƽ���ı���OACB�������
��3�����߶�OC���е�ΪQ��P�˶���ʱ��Ϊt����tΪ��ֵʱ��![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
���𰸡���1��![]() ����2��
����2��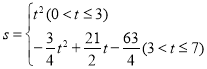 ����
����![]() ʱ��ֱ��EFƽ���ı���OABC���������3����
ʱ��ֱ��EFƽ���ı���OABC���������3����![]() ��
��![]() ʱ��
ʱ��![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
��������
��1������![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ���Լ�
���Լ�![]() ���������ȵó�
���������ȵó�![]() ������Ϊ
������Ϊ![]() �е㣬���ɵó��𰸣�
�е㣬���ɵó��𰸣�
��2���ֱ���ݵ�![]() ʱ����
ʱ����![]() ʱ���������������ε����ʵó�
ʱ���������������ε����ʵó�![]() ��
��![]() �Ĺ�ϵʱ���ɣ�
�Ĺ�ϵʱ���ɣ�
��3�����âٵ�![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ʱ���Լ��ڵ�
ʱ���Լ��ڵ�![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ʱ���������������ε����ʵó�����.
ʱ���������������ε����ʵó�����.
��1��G���������![]() ��
��
��2����C��������![]() ��
��
��OC��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ� ��
��
�֡�![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
�ٵ�![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�ڵ�![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]() ��
��

��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]()
![]()
![]() ��
��
��s��t�ĺ�����ϵʽ�ǣ�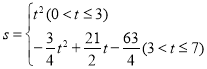
��ֱ��EFƽ���ı���OABC�����ʱ�У�![]() ��
��
�����ã�![]() ��
��
��ã�![]() ��������������ȥ����
��������������ȥ����![]() ��
��
�ʵ�![]() ʱ��ֱ��EFƽ���ı���OABC�������
ʱ��ֱ��EFƽ���ı���OABC�������
��3������ͼ1����P���߶�OQ�ϣ���![]() ʱ��
ʱ��
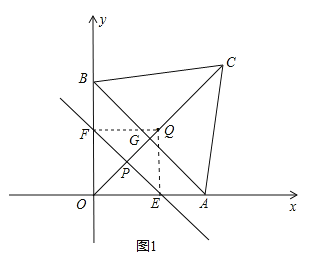
��![]() ��
��
��![]() ��
��
��![]() ��
��
�֡�![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
���ı���OEQF�������Σ�
��![]() ��
��
��![]() ʱ��
ʱ��![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
����ͼ2����P���߶�CQ�ϣ���![]() ʱ��
ʱ��
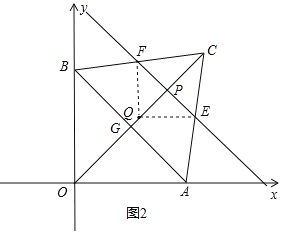
ͬ����֤��![]() ��
��
��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]()
��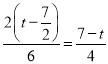 ��
��
��ã�![]() ��
��
�ʵ�![]() ��
��![]() ʱ��
ʱ��![]() Ϊֱ��������
Ϊֱ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Բ�İ뾶OC=2���߶�BC��CD�ǰ�Բ�������ң�BC=CD���ӳ�CD��ֱ��BA���ӳ����ڵ�E����AE=2������BD�ij�Ϊ_______��
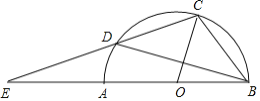
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
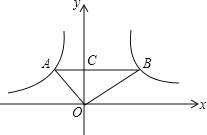
����Ŀ����ͼ����ֱ������ϵ�У�OΪ����ԭ�㣬����![]() ��
��![]() ��ͼ���ϣ��ֱ���A.B���㣬��AB��x���ҽ�y���ڵ�C����OA��OB��S��AOC=
��ͼ���ϣ��ֱ���A.B���㣬��AB��x���ҽ�y���ڵ�C����OA��OB��S��AOC=![]() ��S��BOC=
��S��BOC=![]() �����߶�AB�ij���Ϊ( )
�����߶�AB�ij���Ϊ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У��Խ���AC��BD���ڵ�O������C��BD��ƽ���ߣ�����D��AC��ƽ���ߣ���ֱ���ཻ�ڵ�E��
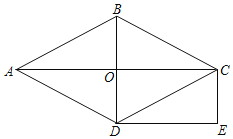
��1����֤���ı���OCED�Ǿ��Σ�
��2����CE��2��DE��3��������ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������y=![]() x2ƽ�Ƶõ�������m��������m������A����6��0����ԭ��O��0��0�������Ķ���ΪP�����ĶԳ�����������y=
x2ƽ�Ƶõ�������m��������m������A����6��0����ԭ��O��0��0�������Ķ���ΪP�����ĶԳ�����������y=![]() x2���ڵ�Q����ͼ����Ӱ���ֵ����Ϊ�� �� ����
x2���ڵ�Q����ͼ����Ӱ���ֵ����Ϊ�� �� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=6��PΪ��CD��һ�㣬�ѡ�BCP��ֱ��BP�۵�������C�۵���C��������BC����AD���ڵ�E������CE��BP���ڵ�Q����CE��BE.
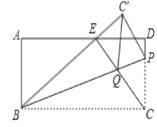
(1)��֤����ABE�ס�DEC��
(2)��AD=13ʱ��AE<DE����CE�ij���
(3)����C��Q��ֱ��д���ı���C��QCP����״��______.��CP=4ʱ������CEEQ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ֱ�������ε�ֽƬ����ֱ�DZ�AC=6cm��BC=8cm���ֽ�ֱ�DZ�AC��ֱ��AD�۵���ʹ������б��AB�ϣ�����AE�غϣ���CD���ڣ����� ��.

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ʾ����ƽ��ֱ������ϵxoy�У��ı���OABC�Ǿ��Σ�OA=4��OC=3������P�ӵ�C������������CB������ÿ��2����λ���ȵ��ٶ��˶���ͬʱ������Q�ӵ�O��������x�������᷽����ÿ��1����λ���ȵ��ٶ��˶������P����Q���˶�ʱ��Ϊt��s����
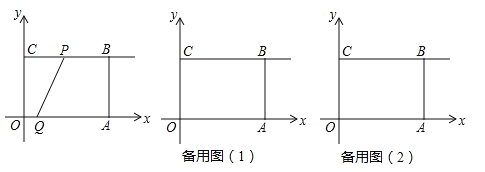
��1����t=1sʱ������O��P��A����������ߵĽ���ʽ��
��2����t=2sʱ����tan��QPA��ֵ��
��3�����߶�PQ���߶�AB�ཻ�ڵ�M����BM=2AMʱ����t��s����ֵ��
��4������CQ������P��Q���˶������У�����CQP�����OABC�ص����ֵ����ΪS����S��t�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O����CBG=��A��CDΪֱ����OC��AB�ཻ�ڵ�E������E��EF��BC������ΪF������BD��
��1����֤��BG���O���У�
��2����![]() ����
����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com