
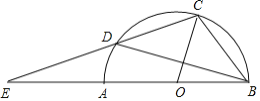
【题目】如图,半圆的半径OC=2,线段BC与CD是半圆的两条弦,BC=CD,延长CD交直径BA的延长线于点E,若AE=2,则弦BD的长为_______.
【答案】![]()
【解析】
连接OD,AD,根据已知可得OC平分∠BCD,根据BC=DC,即可得到BD⊥CO,根据已知可以推得CO⊥BD,再根据AB为直径,继而可得AD//CO,结合AE=AO=2,则可得AD=1,在Rt△ABD中,利用勾股定理即可求得BD的长.
连接OD,AD,
∵BC=CD,BO=DO,
∴∠1=∠2,∠3=∠DBO,
∴∠1+∠3=∠2+∠DBO,∴∠CDO=∠CBO,
∵OC=OB=OD,
∴∠BCO=∠DCO,
∴CO为等腰△BCD的角平分线,
∴CO⊥BD,
∵AB为直径,
∴∠ADB=90°,
∴∠3+∠5=∠3+∠4=90°,
∴∠4=∠5,
∴AD//CO,
∵AE=AO=2,∴AD=![]() CO=1,
CO=1,
在Rt△ABD中,BD=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①,有两个△ABC和△A′B′C′,其中∠C+∠C′=180°,且两个三角形不相似.能否分别用一条直线分割这两个三角形,使△ABC所分割成的两个三角形与△A′B′C′所分割成的两个三角形分别相似?如果能,画出分割线,并标明相等的角;如果不能,请说明理由.
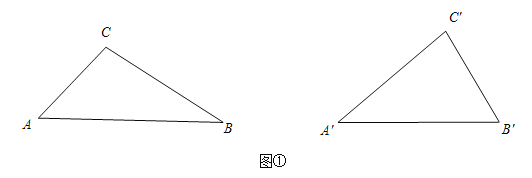
小明经过思考后,尝试从特殊情况入手,画出了当∠C=∠C′=90°时的分割线:
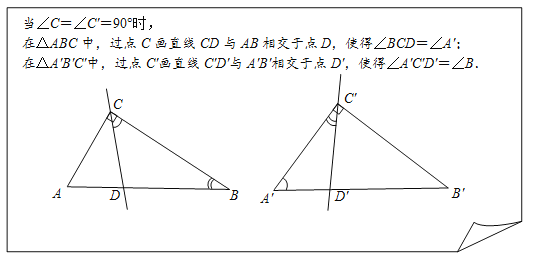
(1)小明在完成画图后给出了如下证明思路,请补全他的证明思路.
由画图可得△BCD∽△ .
由∠A+∠B=90°,∠A′C′D′+∠B′C′D′=90°,∠A′C′D′=∠B,得 .
同理可得:∠B′=∠ACD.
由此得:△ACD∽△ .
(2)当∠C>∠C′时,请在图①的两个三角形中分别画出满足题意的分割线,并标明相等的角.(不写画法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为45°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走4米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度为_____.
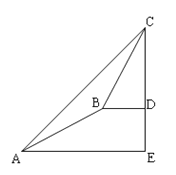
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…,直线ln⊥x轴于点(n,0)(其中n为正整数).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=2x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn.如果△OA1B1的面积记作S,四边形A1A2B2B1的面积记作S1,四边形A2A3B3B2的面积记作S2,…,四边形AnAn+1Bn+1Bn的面积记作Sn,那么S2018=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
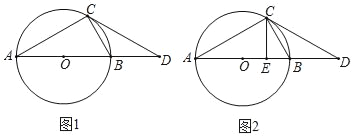
【题目】如图(1),在△ABC中,∠ACB=90°,以AB为直径作⊙O;过点C作直线CD交AB的延长线于点D,且BD=OB,CD=CA.
(1)求证:CD是⊙O的切线.
(2)如图(2),过点C作CE⊥AB于点E,若⊙O的半径为8,∠A=30°,求线段BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
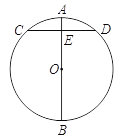
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
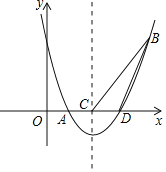
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A,D两点,并经过B点,对称轴交x轴于点C,连接BD,BC,已知A点坐标是(2,0),B点的坐标是(8,6)
x2+bx+c的图象交x轴于A,D两点,并经过B点,对称轴交x轴于点C,连接BD,BC,已知A点坐标是(2,0),B点的坐标是(8,6)
(1)求二次函数的解析式.
(2)求该函数图象的顶点坐标及D点的坐标.
(3)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP=![]() S△BCD?若存在,直接写出所有符合条件的点P的坐标;若不存在.请说明理由.
S△BCD?若存在,直接写出所有符合条件的点P的坐标;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
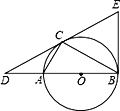
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com