【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动，如图，在点A处测得直立于地面的大树顶端C的仰角为45°，然后沿在同一剖面的斜坡AB行走13米至坡顶B处，然后再沿水平方向行走4米至大树脚底点D处，斜面AB的坡度（或坡比）i=1：2.4，那么大树CD的高度为_____．
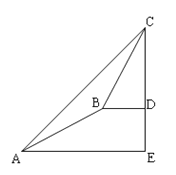
【答案】11
【解析】
可以作BF⊥AE于F，在Rt△ABF中，运用勾股定理，根据各边的数量关系求得AF的长度，就可得到AE的长度；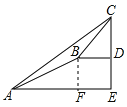
接下来根据已知的AE的长度，在Rt△ACE中，运用三角函数求得CE的长度，进而可知CD的长度.
解：作BF⊥AE于F，如图所示：
则FE=BD=4米，DE=BF.
∵斜面AB的坡度i=1:2.4，
∴AF=2.4BF.
设BF=x米，则AF=2.4x米，
在Rt△ABF中，由勾股定理得：x2+(2.4x)2=132，
解得：x=5，
∴DE=BF=5米，AF=12米，
∴AE=AF+FE=16米.
在Rt△ACE中，CE=AE=16米，
∴CD=CE-DE=16米-5米=11米.
字词句篇与同步作文达标系列答案科目：初中数学 来源： 题型：
【题目】△ABC在平面直角坐标系xOy中的位置如图所示．
（1）作△ABC关于点C成中心对称的△A1B1C1．
（2）将△A1B1C1向右平移4个单位，作出平移后的△A2B2C2．
（3）在x轴上求作一点P，使PA1+PC2的值最小，并写出点P的坐标（不写解答过程，直接写出结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，抛物线C1：y＝ax2+bx+1的顶点坐标为D（1，0）且经过点（0，1），将抛物线C1向右平移1个单位，向下平移1个单位得到抛物线C2，直线y＝x+c，经过点D交y轴于点A，交抛物线C2于点B，抛物线C2的顶点为P．
(1)求抛物线C1的解析式；
(2)如图2，连结AP，过点B作BC⊥AP交AP的延长线于C，设点Q为抛物线上点P至点B之间的一动点，连结BQ并延长交AC于点F，
①当点Q运动到什么位置时，S△PBD×S△BCF＝8？
②连接PQ并延长交BC于点E，试证明：FC（AC+EC）为定值．
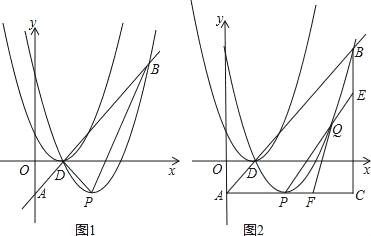
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y，的对应值如下表：
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
（1）根据上表填空：
①抛物线与x轴的交点坐标是_________和_________；
②抛物线经过点（-3，_________）；
（2）试确定抛物线y=ax2+bx+c的解析式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在等腰Rt△ABC中，AC＝BC＝2，点P在以斜边AB为直径的半圆上，M为PC的中点．当点P沿半圆从点A运动至点B时，点M运动的路径长是（ ）
A. π B. 
C. 2 D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
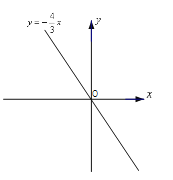
【题目】一次函数y＝
x的图像如图所示，它与二次函数y＝ax2+2ax＋c的图像交于A、B两点（其中点A在点B的左侧），与这个二次函数图像的对称轴交于点C．
（1）求点C的坐标；
（2）设二次函数图像的顶点为D．若点D与点C关于x轴对称，且△ACD的面积等于
，求此二次函数的关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店需要购进甲、乙两种商品共160件，其进价和售价如下表：(注：获利=售价－进价)
(1)若商店计划销售完这批商品后能获利1 100元，请问甲、乙两种商品应分别购进多少件？
(2)若商店计划投入资金少于4300元，且销售完这批商品后获利多于1260元，请问有哪几种购货方案？并指出获利最大的购货方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
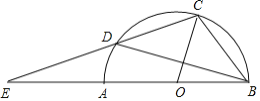
【题目】如图，半圆的半径OC=2，线段BC与CD是半圆的两条弦，BC=CD，延长CD交直径BA的延长线于点E，若AE=2，则弦BD的长为_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
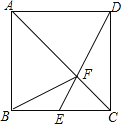
【题目】如图，已知正方形ABCD，点E是BC边的中点，DE与AC相交于点F，连接BF，下列结论：①S△ABF=S△ADF②S△CDF=4S△CEF；③S△ADF=2S△CEF；④S△ADF=2S△CDF，其中正确的是（ ）
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com