
【题目】如图1,抛物线C1:y=ax2+bx+1的顶点坐标为D(1,0)且经过点(0,1),将抛物线C1向右平移1个单位,向下平移1个单位得到抛物线C2,直线y=x+c,经过点D交y轴于点A,交抛物线C2于点B,抛物线C2的顶点为P.
(1)求抛物线C1的解析式;
(2)如图2,连结AP,过点B作BC⊥AP交AP的延长线于C,设点Q为抛物线上点P至点B之间的一动点,连结BQ并延长交AC于点F,
①当点Q运动到什么位置时,S△PBD×S△BCF=8?
②连接PQ并延长交BC于点E,试证明:FC(AC+EC)为定值.
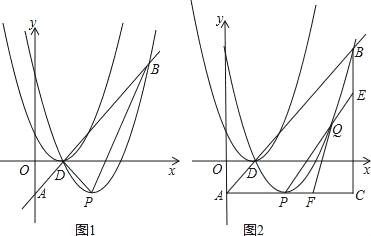
【答案】(1)y=x2﹣2x+1;(2)点Q运动到x轴时,S△PBD×S△BCF=8;②证明见解析.
【解析】
(1)已知顶点D的坐标,设抛物线的顶点式为:y=a(x-1)2,将点(0,1)代入即可;
(2)根据平移规律求出平移后抛物线的顶点坐标,即P(2,-1),根据顶点式,得平移后抛物线解析式y=(x-2)2-1,由解析式,得A(0,-1),B(4,3),可求△DBP的面积;
(3)由QM∥CE,得△PQM∽△PEC,利用相似比求EC,由QN∥FC,得△BQN∽△BFC,利用相似比求FC,已知AC=4,再计算FC(AC+EC)为定值.
(1)把顶点坐标为D(1,0)和点(0,1)坐标代入y=ax2+bx+1,
解得:抛物线的方程为:y=x2﹣2x+1;
(2)抛物线C1向右平移1个单位,向下平移1个单位得到抛物抛物线C1向右平移1个单位,向下平移1个单位得到抛物线C2,
则抛物线C2的方程为:y=(x﹣2)2﹣1=x2﹣4x+3,
此时顶点P坐标为(2,﹣1),A(0,﹣1)、B(4,3),
①则:S△PBD=3,S△BCF=![]() ,
,
设点Q(m,m2﹣4m+3),把Q、B点坐标代入一次函数表达式,
解得:BQ所在的直线方程为:y=mx+(3﹣4m),
则:F(![]() ,﹣1),S△BCF=
,﹣1),S△BCF=![]() FC(yB﹣yC)=
FC(yB﹣yC)=![]() =
=![]() ,
,
则m=3,点Q坐标为:(3,0),即:点Q运动到x轴时,S△PBD×S△BCF=8;
②如下图所示,过Q点分别作AC、BC的垂线QM、QN,
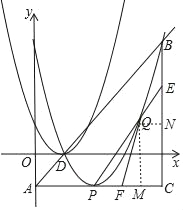
设:Q(t,t2﹣4t+3),则QM=CN=(t﹣2)2,MC=QN=4﹣t,
∵QM∥CE,∴![]() =
=![]() ,则:
,则:![]() =
=![]() ,解得:EC=2t﹣4,
,解得:EC=2t﹣4,
∵QN∥FC,![]() ,则:FC=
,则:FC=![]() ,而AC=4,
,而AC=4,
∴FC(AC+EC)=![]() (4+2t﹣4)=8,为定值.
(4+2t﹣4)=8,为定值.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
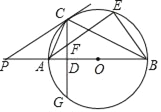
【题目】如图,AB为⊙O的直径,P是BA延长线上一点,CG是⊙O的弦∠PCA=∠ABC,CG⊥AB,垂足为D
(1)求证:PC是⊙O的切线;
(2)求证:![]() ;
;
(3)过点A作AE∥PC交⊙O于点E,交CD于点F,连接BE,若sin∠P=![]() ,CF=5,求BE的长.
,CF=5,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=![]() S△BOC,求点D的坐标.
S△BOC,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“我运动,我快乐”的技能比赛培训活动中,在相同条件下,对甲、乙两名同学的“单手运球”项目进行了5次测试,测试成绩(单位:分)如下:根据右图判断正确的是( )

A.甲成绩的平均分低于乙成绩的平均分;
B.甲成绩的中位数高于乙成绩的中位数;
C.甲成绩的众数高于乙成绩的众数;
D.甲成绩的方差低于乙成绩的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是BC边所在直线上一动点(不与点B、C重合),过点B作BF⊥DE,交射线DE于点F,连接CF.
(1)如图,当点E在线段BC上时,∠BDF=α.
①按要求补全图形;
②∠EBF=______________(用含α的式子表示);
③判断线段 BF,CF,DF之间的数量关系,并证明.
(2)当点E在直线BC上时,直接写出线段BF,CF,DF之间的数量关系,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
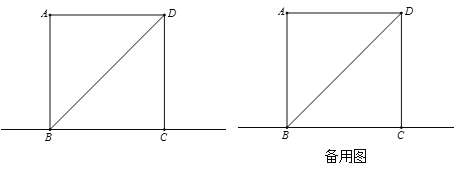
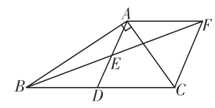
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com