
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЕуEЪЧBCБпЫљдкжБЯпЩЯвЛЖЏЕуЃЈВЛгыЕуBЁЂCжиКЯЃЉЃЌЙ§ЕуBзїBFЁЭDEЃЌНЛЩфЯпDEгкЕуFЃЌСЌНгCFЃЎ
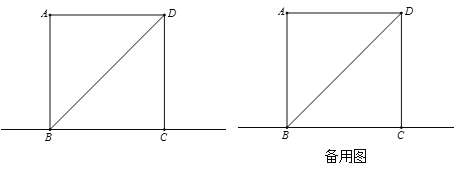
ЃЈ1ЃЉШчЭМЃЌЕБЕуEдкЯпЖЮBCЩЯЪБЃЌЁЯBDF=ІСЃЎ
ЂйАДвЊЧѓВЙШЋЭМаЮЃЛ
ЂкЁЯEBF=______________ЃЈгУКЌІСЕФЪНзгБэЪОЃЉЃЛ
ЂлХаЖЯЯпЖЮ BFЃЌCFЃЌDFжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ
ЃЈ2ЃЉЕБЕуEдкжБЯпBCЩЯЪБЃЌжБНгаДГіЯпЖЮBFЃЌCFЃЌDFжЎМфЕФЪ§СПЙиЯЕЃЌВЛашжЄУїЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйМћНтЮіЃЛЂк45Ёу-ІСЃЛЂлЯпЖЮBFЃЌCFЃЌDFжЎМфЕФЪ§СПЙиЯЕЪЧ![]() ЃЌжЄУїМћНтЮіЃЛЃЈ2ЃЉ
ЃЌжЄУїМћНтЮіЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
ЁОНтЮіЁП
(1)ЂйгЩЬтвтВЙШЋЭМаЮМДПЩЃЛ
ЂкгЩе§ЗНаЮЕФаджЪЕУГі![]() ЃЌгЩШ§НЧаЮЕФЭтНЧаджЪЕУГі
ЃЌгЩШ§НЧаЮЕФЭтНЧаджЪЕУГі![]() ЃЌгЩжБНЧШ§НЧаЮЕФаджЪЕУГі
ЃЌгЩжБНЧШ§НЧаЮЕФаджЪЕУГі![]() МДПЩЃЛ
МДПЩЃЛ
ЂлдкDFЩЯНиШЁDM=BFЃЌСЌНгCMЃЌжЄУїЁїCDMЁеЁїCBFЃЌЕУГіCM=CFЃЌЁЯDCM=ЁЯBCFЃЌЕУГіMF=![]() МДПЩЕУГіНсТлЃЛ
МДПЩЕУГіНсТлЃЛ
(2)ЗжШ§жжЧщПіЃКЂйЕБЕуEдкЯпЖЮBCЩЯЪБЃЌDF=BF+![]() ЃЌРэгЩЭЌ(1)ЂлЃЛ
ЃЌРэгЩЭЌ(1)ЂлЃЛ
ЂкЕБЕуEдкЯпЖЮBCЕФбгГЄЯпЩЯЪБЃЌBF=DF+![]() ЃЌдкBF_ЩЯНиШЁBM=DFЃЌСЌНгCM.ЭЌ(1)ЂлЕУЁїCBMЁеЁїCDFЕУГіCM=CFЃЌЁЯBCM=ЁЯDCFЃЌжЄУїЁїCMFЪЧЕШбќжБНЧШ§НЧаЮЃЌЕУГіMF=
ЃЌдкBF_ЩЯНиШЁBM=DFЃЌСЌНгCM.ЭЌ(1)ЂлЕУЁїCBMЁеЁїCDFЕУГіCM=CFЃЌЁЯBCM=ЁЯDCFЃЌжЄУїЁїCMFЪЧЕШбќжБНЧШ§НЧаЮЃЌЕУГіMF=![]() ЃЌМДПЩЕУГіНсТлЃЛ
ЃЌМДПЩЕУГіНсТлЃЛ
ЂлЕБЕуEдкЯпЖЮCBЕФбгГЄЯпЩЯЪБЃЌBF+DF=![]() ЃЌдкDFЩЯНиШЁDM=BFЃЌСЌНгCMЃЌЭЌ(1)ЂлЕУ:ACDMЁеЁїCBFЕУГіCM=CFЃЌЁЯDCM=ЁЯBCFЃЌжЄУїЁїCMFЪЧЕШбќжБНЧШ§НЧаЮЃЌЕУГіMF=
ЃЌдкDFЩЯНиШЁDM=BFЃЌСЌНгCMЃЌЭЌ(1)ЂлЕУ:ACDMЁеЁїCBFЕУГіCM=CFЃЌЁЯDCM=ЁЯBCFЃЌжЄУїЁїCMFЪЧЕШбќжБНЧШ§НЧаЮЃЌЕУГіMF=![]() ЃЌМДПЩЕУГіНсТл.
ЃЌМДПЩЕУГіНсТл.
ЃЈ1ЃЉЂйШчЭМЃЌ

ЂкЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрЁЯABC=90ЁуЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпBFЁЭDE,
ЁрЁЯBFE=90ЁуЃЌ
Ёр![]() ,
,
ЙЪД№АИЮЊЃК45Ёу-ІСЃЛ
ЂлЯпЖЮBFЃЌCFЃЌDFжЎМфЕФЪ§СПЙиЯЕЪЧ![]() .
.
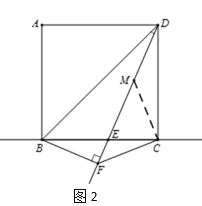
жЄУїШчЯТЃКдкDFЩЯНиШЁDM=BFЃЌСЌНгCM.ШчЭМ2ЫљЪОЃЌ
Ёп е§ЗНаЮABCDЃЌ
Ёр BC=CDЃЌЁЯBDC=ЁЯDBC=45ЁуЃЌЁЯBCD=90Ёу
ЁрЁЯCDM=ЁЯCBF=45Ёу-ІСЃЌ
ЁрЁїCDMЁеЁїCBFЃЈSASЃЉ.
Ёр DM=BFЃЌ CM=CFЃЌЁЯDCM=ЁЯBCF.
Ёр ЁЯMCF =ЁЯBCF+ЁЯMCE
=ЁЯDCM+ЁЯMCE
=ЁЯBCD=90ЁуЃЌ
Ёр MF =![]() .
.
Ёр![]()
ЃЈ2ЃЉЗжШ§жжЧщПіЃКЂйЕБЕуEдкЯпЖЮBCЩЯЪБЃЌDF=BF+![]() ЃЌРэгЩЭЌ(1)ЂлЃЛ
ЃЌРэгЩЭЌ(1)ЂлЃЛ
ЂкЕБЕуEдкЯпЖЮBCЕФбгГЄЯпЩЯЪБЃЌBF=DF+![]() ЃЌРэгЩШчЯТЃК
ЃЌРэгЩШчЯТЃК
дкBFЩЯНиШЁBM=DFЃЌСЌНгCMЃЌШчЭМ3ЫљЪОЃЌ
ЭЌ(1)ЂлЃЌЕУЃКЁїCBMЁеЁїCDF(SAS)ЃЌ
ЁрCM=CFЃЌЁЯBCM=ЁЯDCF.
ЁрЁЯMCF=ЁЯDCF+ЁЯMCD=ЁЯBCM+ЁЯMCD=ЁЯBCD=90ЁуЃЌ
ЁрЁїCMFЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрMF=![]() ЃЌ
ЃЌ
ЁрBF=BM+MF=DF+![]() ЃЛ
ЃЛ
ЂлЕБЕуEдкЯпЖЮCBЕФбгГЄЯпЩЯЪБЃЌBF+DF=![]() ЃЛРэгЩШчЯТЃК
ЃЛРэгЩШчЯТЃК
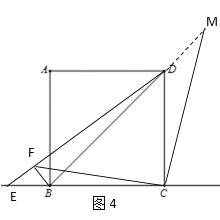
дкDFЩЯНиШЁDM=BFЃЌСЌНгCMЃЌШчЭМ4ЫљЪОЃЌ
ЭЌЃЈ1ЃЉЂлЕУЃКЁїCDMЁеЁїCBFЃЌ
ЁрCM=CFЃЌЁЯDCM=ЁЯBCFЃЌ
ЁрЁЯMCF=ЁЯDCF+ЁЯMCD=ЁЯDCF+ЁЯBCF=ЁЯBCD=90ЁуЃЌ
ЁрЁїCMFЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрMF=![]() ,
,
МДDM+DF=![]() ЃЌ
ЃЌ
ЁрBF+DF=![]() ;
;
злЩЯЫљЪіЃЌЕБЕуEдкжБЯпBCЩЯЪБЃЌЯпЖЮBFЃЌCFЃЌDFжЎМфЕФЪ§ЕМЙиЯЕЮЊЃК![]() ЃЌЛђ
ЃЌЛђ![]() ЃЌЛђ
ЃЌЛђ![]() .
.




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧЕШБпШ§НЧаЮ
ЪЧЕШБпШ§НЧаЮ![]() ФквЛЕуЃЌНЋЯпЖЮ
ФквЛЕуЃЌНЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ60ЁуЕУЕНЯпЖЮ
ЫГЪБеыа§зЊ60ЁуЕУЕНЯпЖЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎШє
ЃЎШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђЫФБпаЮ
ЃЌдђЫФБпаЮ![]() ЕФУцЛ§ЮЊ___________ЃЎ
ЕФУцЛ§ЮЊ___________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
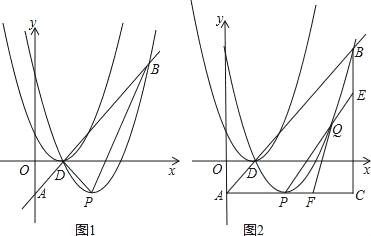
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпC1ЃКyЃНax2+bx+1ЕФЖЅЕузјБъЮЊDЃЈ1ЃЌ0ЃЉЧвОЙ§ЕуЃЈ0ЃЌ1ЃЉЃЌНЋХзЮяЯпC1ЯђгвЦНвЦ1ИіЕЅЮЛЃЌЯђЯТЦНвЦ1ИіЕЅЮЛЕУЕНХзЮяЯпC2ЃЌжБЯпyЃНx+cЃЌОЙ§ЕуDНЛyжсгкЕуAЃЌНЛХзЮяЯпC2гкЕуBЃЌХзЮяЯпC2ЕФЖЅЕуЮЊPЃЎ
(1)ЧѓХзЮяЯпC1ЕФНтЮіЪНЃЛ
(2)ШчЭМ2ЃЌСЌНсAPЃЌЙ§ЕуBзїBCЁЭAPНЛAPЕФбгГЄЯпгкCЃЌЩшЕуQЮЊХзЮяЯпЩЯЕуPжСЕуBжЎМфЕФвЛЖЏЕуЃЌСЌНсBQВЂбгГЄНЛACгкЕуFЃЌ
ЂйЕБЕуQдЫЖЏЕНЪВУДЮЛжУЪБЃЌSЁїPBDЁСSЁїBCFЃН8ЃП
ЂкСЌНгPQВЂбгГЄНЛBCгкЕуEЃЌЪджЄУїЃКFCЃЈAC+ECЃЉЮЊЖЈжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
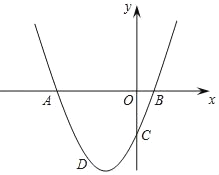
ЁОЬтФПЁПвбжЊЃЌХзЮяЯпyЃНax2+2ax+cгыyжсНЛгкЕуCЃЌгыxжсНЛгкAЃЌBСНЕуЃЌЕуAдкЕуBзѓВрЃЎЕуBЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌOCЃН3OBЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБaЃО0ЪБЃЌШчЭМЫљЪОЃЌШєЕуDЪЧЕкШ§ЯѓЯоЗНХзЮяЯпЩЯЕФЖЏЕуЃЌЩшЕуDЕФКсзјБъЮЊmЃЌШ§НЧаЮADCЕФУцЛ§ЮЊSЃЌЧѓГіSгыmЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіздБфСПmЕФШЁжЕЗЖЮЇЃЛЧыЮЪЕБmЮЊКЮжЕЪБЃЌSгазюДѓжЕЃПзюДѓжЕЪЧЖрЩйЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
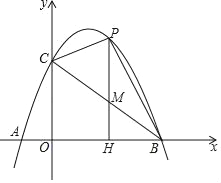
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§yЃНax2+bx+cЕФЭМЯѓгыxжсЯрНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсЯрНЛгкЕуCЃЈ0ЃЌ3ЃЉ
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФБэДяЪНВЂжБНгаДГіЖЅЕузјБъЃЛ
ЃЈ2ЃЉШєPЪЧЕквЛЯѓЯоФкетИіЖўДЮКЏЪ§ЕФЭМЯѓЩЯШЮвтвЛЕуЃЌPHЁЭxжсгкЕуHЃЌгыBCНЛгкЕуMЃЌСЌНгPCЃЎЩшЕуPЕФКсзјБъЮЊt
ЂйЧѓЯпЖЮPMЕФзюДѓжЕЃЛ
ЂкSЁїPBMЃКSЁїMHBЃН1ЃК2ЪБЃЌЧѓtжЕЃЛ
ЂлЕБЁїPCMЪЧЕШбќШ§НЧаЮЪБЃЌжБНгаДЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪае§дкПЊеЙЁАЪГЦЗАВШЋГЧЪаЁБДДНЈЛюЖЏЃЌЮЊСЫНтбЇЩњЖдЪГЦЗАВШЋжЊЪЖЕФСЫНтЧщПіЃЌбЇаЃЫцЛњГщШЁСЫВПЗжбЇЩњНјааЮЪОэЕїВщЃЌНЋЕїВщНсЙћАДееЁА![]() ЗЧГЃСЫНтЁЂ
ЗЧГЃСЫНтЁЂ![]() СЫНтЁЂ
СЫНтЁЂ![]() СЫНтНЯЩйЁЂ
СЫНтНЯЩйЁЂ![]() ВЛСЫНтЁБЫФРрЗжБ№НјааЭГМЦЃЌВЂЛцжЦСЫЯТСаСНЗљЭГМЦЭМЃЈВЛЭъећЃЉЃЎЧыИљОнЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ВЛСЫНтЁБЫФРрЗжБ№НјааЭГМЦЃЌВЂЛцжЦСЫЯТСаСНЗљЭГМЦЭМЃЈВЛЭъећЃЉЃЎЧыИљОнЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
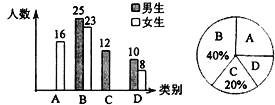
ЃЈ1ЃЉДЫДЮЙВЕїВщСЫ__________УћбЇЩњЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжа![]() ЫљдкЩШаЮЕФдВаФНЧЮЊ__________ЁуЃЛ
ЫљдкЩШаЮЕФдВаФНЧЮЊ__________ЁуЃЛ
ЃЈ3ЃЉНЋЩЯУцЕФЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ4ЃЉШєИУаЃЙВга1600УћбЇЩњЃЌЧыФуЙРМЦЖдЪГЦЗАВШЋжЊЪЖЁАЗЧГЃСЫНтЁБЕФбЇЩњЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЁїABCдкжБНЧзјБъЦНУцФкЃЌШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈ1ЃЌ0ЃЉЁЂBЃЈ3ЃЌ2ЃЉЁЂCЃЈ0ЃЌ1ЃЉЃЈе§ЗНаЮЭјИёжаУПИіаЁе§ЗНаЮЕФБпГЄЪЧвЛИіЕЅЮЛГЄЖШЃЉЃЎ
(1)биxжсЯђзѓЦНвЦ2ИіЕЅЮЛЃЌЕУЕНЁїA1B1C1ЃЌВЛЛЭМжБНгаДГіЗЂЩњБфЛЏКѓЕФ![]() ЕуЕФзјБъЁЃЕу
ЕуЕФзјБъЁЃЕу![]() ЕФзјБъЪЧЁЁЃЛ
ЕФзјБъЪЧЁЁЃЛ
(2)вдAЕуЮЊЮЛЫЦжааФ,дкЭјИёФкЛГіЁїA2B2C2ЃЌЪЙЁїA2B2C2гыЁїABCЮЛЫЦЃЌЧвЮЛЫЦБШЮЊ2ЃК1ЃЌдђЕу![]() ЕФзјБъЪЧЁЁЁЁЃЛ
ЕФзјБъЪЧЁЁЁЁЃЛ
(3) ЁїA2B2C2ЕФУцЛ§ЪЧЁЁЦНЗНЕЅЮЛЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГИжЬњГЇНёФъ1дТЗнИжВњСПЮЊ5000ЖжЃЌ3дТЗнЩЯЩ§ЕН7200ЖжЃЌЩшЦНОљУПдТдіГЄЕФАйЗжТЪЮЊ![]() ЃЌИљОнЬтвтЕУЗНГЬЃЈ ЃЉ
ЃЌИљОнЬтвтЕУЗНГЬЃЈ ЃЉ
A. 5000(1+x)+5000(1+x)2=7200 B. 5000(1+x2)=7200
C. 5000(1+x)2=7200 D. 5000+5000(1+x)2=7200
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
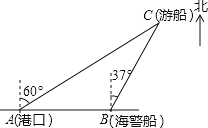
ЁОЬтФПЁП вЛЫвЙлЙтгЮДЌДгИлПкAвдББЦЋЖЋ60ЁуЕФЗНЯђГіИлЙлЙтЃЌКНаа80КЃРяжСCДІЪБЗЂЩњСЫВрЗГСДЌЪТЙЪЃЌСЂМДЗЂГіСЫЧѓОШаХКХЃЌвЛЫвдкИлПке§ЖЋЗНЯђЕФКЃОЏДЌНгЕНЧѓОШаХКХЃЌВтЕУЪТЙЪДЌдкЫќЕФББЦЋЖЋ37ЁуЗНЯђЃЌТэЩЯвд40КЃРяУПаЁЪБЕФЫйЖШЧАЭљОШдЎЃЌЧѓКЃОЏДЌЕНДѓЪТЙЪДЌCДІЫљашЕФДѓдМЪБМфЃЎЃЈЮТмАЬсЪОЃКsin53ЁуЁж0.8ЃЌcos53ЁуЁж0.6ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com