
【题目】如图,在矩形ABCD中,AB=6,P为边CD上一点,把△BCP沿直线BP折叠,顶点C折叠到C′,连接BC′与AD交于点E,连接CE与BP交于点Q,若CE⊥BE.
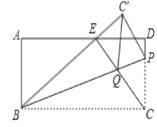
(1)求证:△ABE∽△DEC;
(2)当AD=13时,AE<DE,求CE的长;
(3)连接C′Q,直接写出四边形C′QCP的形状:______.当CP=4时,并求CEEQ的值.
【答案】(1)证明见解析;(2)3![]() ;(3)菱形,24.
;(3)菱形,24.
【解析】
(1)由题意可得∠AEB+∠CED=90°,且∠ECD+∠CED=90°,可得∠AEB=∠ECD,且∠A=∠D=90°,则可证△ABE∽△DEC;
(2)设AE=x,则DE=13x,由相似三角形的性质可得![]() ,即:
,即:![]() ,可求x的值,即可得DE=9,根据勾股定理可求CE的长;
,可求x的值,即可得DE=9,根据勾股定理可求CE的长;
(3)由折叠的性质可得CP=C′P,CQ=C′Q,∠C′PQ=∠CPQ,∠BC′P=∠BCP=90,由平行线的性质可得∠C′PQ=∠CQP=∠CPQ,即可得CQ=CP=C′Q=C′P,则四边形C′QCP是菱形,通过证△C′EQ∽△EDC,可得![]() ,即可求CEEQ的值.
,即可求CEEQ的值.
证明:(1)∵CE⊥BE,
∴∠BEC=90°,
∴∠AEB+∠CED=90°,
又∵∠ECD+∠CED=90°,
∴∠AEB=∠ECD,
又∵∠A=∠D=90°,
∴△ABE∽△DEC
(2)设AE=x,则DE=13x,
由(1)知:△ABE∽△DEC,
∴![]() ,即:
,即:![]()
∴x![]() 13x+36=0,
13x+36=0,
∴x![]() =4,x
=4,x![]() =9,
=9,
又∵AE<DE
∴AE=4,DE=9,
在Rt△CDE中,由勾股定理得:![]() .
.
(3)∵折叠,
∴CP=C′P,CQ=C′Q,∠C′PQ=∠CPQ,∠BC′P=∠BCP=90°,
∵CE⊥BC′,∠BC′P=90°,
∴CE∥C′P,
∴∠C′PQ=∠CQP,
∴∠CQP=∠CPQ,
∴CQ=CP,
∴CQ=CP=C′Q=C′P,
∴四边形C′QCP是菱形,
故答案为:菱形
∵四边形C′QCP是菱形,
∴C′Q∥CP,C′Q=CP,∠EQC′=∠ECD
又∵∠C′EQ=∠D=90°,
∴△C′EQ∽△EDC
∴![]()
∴CEEQ=DCC′Q=6×4=24


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整统计图.
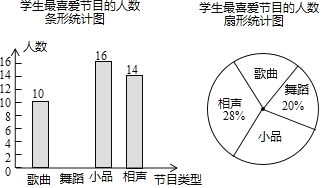
请你根据图中信息,回答下列问题:
(1)本次共调查了 名学生.
(2)在扇形统计图中,“歌曲”所在扇形的圆心角等于 度.
(3)补全条形统计图(标注频数).
(4)根据以上统计分析,估计该校2000名学生中最喜爱小品的人数为 人.
(5)九年一班和九年二班各有2名学生擅长舞蹈,学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排,那么抽取的2名学生恰好来自同一个班级的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
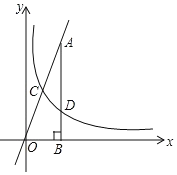
(1)求反比例函数的表达式;
(2)求点C的坐标;
(3)在y轴上确定一点M,使点M到C,D两点距离之和d=MC+MD最小,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6![]() ,BC=3
,BC=3![]() 动点P从点A出发,沿AC以每秒4个单位长度的速度向终点C运动.过点P(不与点A、C重合)作EF⊥AC,交AB或BC于点E,交AD或DC于点F,以EF为边向右作正方形EFGH设点P的运动时间为t秒.
动点P从点A出发,沿AC以每秒4个单位长度的速度向终点C运动.过点P(不与点A、C重合)作EF⊥AC,交AB或BC于点E,交AD或DC于点F,以EF为边向右作正方形EFGH设点P的运动时间为t秒.
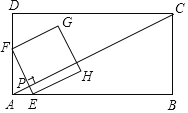
(1)①AC= .②当点F在AD上时,用含t的代数式直接表示线段PF的长 .
(2)当点F与点D重合时,求t的值.
(3)设方形EFGH的周长为l,求l与t之间的函数关系式.
(4)直接写出对角线AC所在的直线将正方形EFGH分成两部分图形的面积比为1:2时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
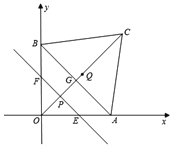
【题目】已知点A,B分别在x轴和y轴上,且![]() ,点C的坐标是
,点C的坐标是![]() ,AB与OC相交于点G.点P从O出发以每秒1个单位的速度从O运动到C,过P作直线
,AB与OC相交于点G.点P从O出发以每秒1个单位的速度从O运动到C,过P作直线![]() 分别交OA,OB或AC,BC于E,F.解答下列问题:
分别交OA,OB或AC,BC于E,F.解答下列问题:
(1)直接写出点G的坐标;
(2)若点P运动的时间为t,直线EF在四边形OACB内扫过的面积为s,请求出s与t的函数关系式;并求出当t为何值时,直线EF平分四边形OACB的面积;
(3)设线段OC的中点为Q,P运动的时间为t,求当t为何值时,![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.从1,2,3,4,5中随机取出一个数,取得偶数的可能性比取得奇数的大
B.若甲组数据的方差S甲2=0.31,乙组数据的方差S乙2=0.02,则甲组数据比乙组数据稳定
C.数据﹣2,1,3,4,4,5的中位数是4
D.了解重庆市初中学生的视力情况,适宜采用抽样调查的方法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有黄球、黑球和红球共40个,它们除颜色外都相同,其中红球有22个,且经过试验发现摸出一个球为黄球的频率接近0.125 。
⑴求袋中有多少个黑球;
⑵现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个球是黄球的概率达到![]() ,问至少取出了多少个黑球?
,问至少取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商家按标价销售工艺品时,每件可获利![]() 元,按标价的八五新销售工艺品
元,按标价的八五新销售工艺品![]() 件与将标价降低
件与将标价降低![]() 元销售这种工艺品
元销售这种工艺品![]() 件所获利润相等.
件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少?
(2)若每件工艺品按此进价进货,标价销售,商家每天可卖出工艺品![]() 件,若每件工艺品降价
件,若每件工艺品降价![]() 元,则每天可多卖出该工艺品
元,则每天可多卖出该工艺品![]() 件,间每件降价多少元销售,每天获得利润最大?获得最大利润是多少元?
件,间每件降价多少元销售,每天获得利润最大?获得最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com