
【题目】一商家按标价销售工艺品时,每件可获利![]() 元,按标价的八五新销售工艺品
元,按标价的八五新销售工艺品![]() 件与将标价降低
件与将标价降低![]() 元销售这种工艺品
元销售这种工艺品![]() 件所获利润相等.
件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少?
(2)若每件工艺品按此进价进货,标价销售,商家每天可卖出工艺品![]() 件,若每件工艺品降价
件,若每件工艺品降价![]() 元,则每天可多卖出该工艺品
元,则每天可多卖出该工艺品![]() 件,间每件降价多少元销售,每天获得利润最大?获得最大利润是多少元?
件,间每件降价多少元销售,每天获得利润最大?获得最大利润是多少元?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,P为边CD上一点,把△BCP沿直线BP折叠,顶点C折叠到C′,连接BC′与AD交于点E,连接CE与BP交于点Q,若CE⊥BE.
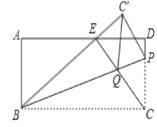
(1)求证:△ABE∽△DEC;
(2)当AD=13时,AE<DE,求CE的长;
(3)连接C′Q,直接写出四边形C′QCP的形状:______.当CP=4时,并求CEEQ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知第一象限内的点A在反比例函数y=![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=![]() 的图象上,且OA⊥OB,cosA=
的图象上,且OA⊥OB,cosA=![]() ,则k的值为( )
,则k的值为( )

A. -3 B. -6 C. -4 D. -![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,直角边![]() ,
,![]() ,设P、Q分别为AB,BC上的动点,点P自点A沿AB方向向点B作匀速移动且速度为每秒2cm,同时点Q自点B沿BC方向向点C作匀速移动且速度为每秒1cm,当P点到达B点时,Q点就停止移动.设P,Q移动的时间t秒.
,设P、Q分别为AB,BC上的动点,点P自点A沿AB方向向点B作匀速移动且速度为每秒2cm,同时点Q自点B沿BC方向向点C作匀速移动且速度为每秒1cm,当P点到达B点时,Q点就停止移动.设P,Q移动的时间t秒.
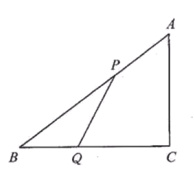
(1)写出![]() 的面积S(
的面积S(![]() )与时间t(s)之间的函数表达式,并写出t的取值范围.
)与时间t(s)之间的函数表达式,并写出t的取值范围.
(2)当t为何值时,![]() 为等腰三角形?
为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,连接BD.
(1)求证:BG与⊙O相切;
(2)若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第五代移动电话通信行动标准,也称第五代移动通信技术,外语缩写:5G.也是4G之后的延伸,正在研究中,5G网络的理论下行速度为10Gb/s(相当于下载速度1.25GB/s).2019年1月24日,华为发布了迄今最强大的5G基带芯片Balong500,同时,还发布了全球最快CPE,支持智能家居连接.中国5G技术的研发带来了社会生产力和社会关系的重大改变,它是国人的骄傲….小明组织了几位同学就5G手机面世后自己居住的小区使用手机的居民是否立即改用5G手机问题,随机对本小区的部分使用手机的居民进行了问卷调查(分五类:A表示非常期待体验,将立即使用;B表示担心费用太高消费不起,但还是要体验,将立即使用;C表示怕技术不成熟,造成经济损失,但还是要体验,将立即使用;D表示先等待一段时间后再说,暂时不体验,不立即使用;E表示其它原因不体验,不立即使用).根据调查结果分别绘制了如下两个统计图,请根据图中提供的信息解答下列问题:

(1)随机被调查的居民总人数为 人,m= ,扇形统计图中A类所对应扇形的园心角为 度;
(2)请根据统计数据补全条形统计图;
(3)若小区有使用手机的居民共约8000人,请估计约有多少居民在5G手机面世后不立即使用5G手机?若通讯公司在5G手机面世后第一个月在本小区的业务目标是最多2000手机用户不使用5G手机,请根据计算结果帮助公司拟定一条宣传建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,点O为其中心.将其绕点O顺时针旋转45°后得到正方形A'B'C'D',则旋转前后两正方形重叠部分构成的多边形的周长为( )(参考计算:![]() )
)
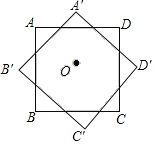
A.16﹣8![]() B.16
B.16![]() ﹣16C.12﹣8
﹣16C.12﹣8![]() D.16
D.16![]() ﹣12
﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
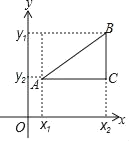
【题目】阅读理解:在平面直角坐标系中,任意两点A(x1,y1),B(x2,y2)之间的位置关系有以下三种情形;
①如果AB∥x轴,则y1=y2,AB=|x1﹣x2|
②如果AB∥y轴,则x1=x2,AB=|y1﹣y2|
③如果AB与x轴、y轴均不平行,如图,过点A作与x轴的平行线与过点B作与y轴的平行线相交于点C,则点C坐标为(x2,y1),由①得AC=|x1﹣x2|;由②得BC=|y1﹣y2|;根据勾股定理可得平面直角坐标系中任意两点的距离公式AB=![]() .
.
小试牛刀:
(1)若点A坐标为(﹣2,3),B点坐标为(3,3)则AB= ;
(2)若点A坐标为(3,2),B点坐标为(3,﹣4)则AB= ;
(3)若点A坐标为(3,2),B点坐标为(7,﹣1)则AB= ;
学以致用:
若点A坐标为(2,2),点B坐标为(4,4),点P是x轴上的动点,当AP+PB取得最小值时点P的坐标为 并求出AP+PB最小值= ;
挑战自我:
已知M=![]() ,N=
,N=![]() 根据数形结合,直接写出M的最小值= ;N的最大值= ;
根据数形结合,直接写出M的最小值= ;N的最大值= ;
查看答案和解析>>
科目:初中数学 来源: 题型:
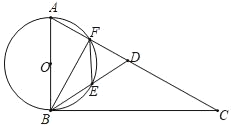
【题目】如图,D为直角△ABC中斜边AC上一点,且AB=AD,以AB为直径的⊙O交AD于点F,交BD于点E,连接BF,BF.
(1)求证:BE=FE;
(2)求证:∠AFE=∠BDC;
(3)已知:sin∠BAE=![]() ,AB=6,求BC的长.
,AB=6,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com