
【题目】阅读理解:在平面直角坐标系中,任意两点A(x1,y1),B(x2,y2)之间的位置关系有以下三种情形;
①如果AB∥x轴,则y1=y2,AB=|x1﹣x2|
②如果AB∥y轴,则x1=x2,AB=|y1﹣y2|
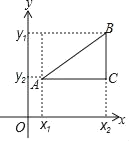
③如果AB与x轴、y轴均不平行,如图,过点A作与x轴的平行线与过点B作与y轴的平行线相交于点C,则点C坐标为(x2,y1),由①得AC=|x1﹣x2|;由②得BC=|y1﹣y2|;根据勾股定理可得平面直角坐标系中任意两点的距离公式AB=![]() .
.
小试牛刀:
(1)若点A坐标为(﹣2,3),B点坐标为(3,3)则AB= ;
(2)若点A坐标为(3,2),B点坐标为(3,﹣4)则AB= ;
(3)若点A坐标为(3,2),B点坐标为(7,﹣1)则AB= ;
学以致用:
若点A坐标为(2,2),点B坐标为(4,4),点P是x轴上的动点,当AP+PB取得最小值时点P的坐标为 并求出AP+PB最小值= ;
挑战自我:
已知M=![]() ,N=
,N=![]() 根据数形结合,直接写出M的最小值= ;N的最大值= ;
根据数形结合,直接写出M的最小值= ;N的最大值= ;
【答案】小试牛刀:(1)5;(2)6;(3)5;学以致用:(![]() ,0),2
,0),2![]() ;挑战自我: 3
;挑战自我: 3![]() ;2
;2![]() .
.
【解析】
小试牛刀:(1)利用两点间的距离公式AB=|x1-x2|进行解答;
(2)利用两点间的距离公式AB=|y1-y2|进行解答;
(3)利用两点间的距离公式AB=![]() 进行解答;
进行解答;
学以致用:利用轴对称的性质求得点P的坐标以及AP+PB的最小值;
挑战自我:利用M、N所表示的几何意义解答.
小试牛刀:(1)AB=|x1﹣x2|=|3﹣(﹣2)|=5.
(2)AB=|y1﹣y2|=|﹣4﹣2|=6.
(3)AB=![]() =
=![]() =5.
=5.
学以致用:如图,
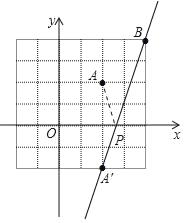
∵点A坐标为(2,2),
∴点A关于x轴对称的点A′的坐标是(2,﹣2),
连接A′B,直线A′B与x轴的交点即为点P.
设直线A′B为y=kx+b(k≠0),则![]() ,
,
解得![]() .
.
∴直线A′B为y=3x﹣8.
令y=0,则x=![]() ,
,
即P(![]() ,0),
,0),
此时AP+PB=A′B=![]() .
.
挑战自我:M=![]() ,
,
当M取最小值时,M表示点(x,0)与点(6,4)的距离与点(x,0)与点 (3,2)的距离之和(或M表示点(x,0)与点(6,﹣4)的距离与点(x,0)与点 (3,﹣2)的距离之和),
此时M最小值=![]() .
.
N=![]() ,
,
当N取最大值时,N表示点(x,0)与点(6,﹣4)的距离与点(x,0)与点 (3,2)的距离之差(或M表示点(x,0)与点(6,﹣4)的距离与点(x,0)与点 (3,2)的距离之差),
此时M最小值=![]() .
.


科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有黄球、黑球和红球共40个,它们除颜色外都相同,其中红球有22个,且经过试验发现摸出一个球为黄球的频率接近0.125 。
⑴求袋中有多少个黑球;
⑵现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个球是黄球的概率达到![]() ,问至少取出了多少个黑球?
,问至少取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商家按标价销售工艺品时,每件可获利![]() 元,按标价的八五新销售工艺品
元,按标价的八五新销售工艺品![]() 件与将标价降低
件与将标价降低![]() 元销售这种工艺品
元销售这种工艺品![]() 件所获利润相等.
件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少?
(2)若每件工艺品按此进价进货,标价销售,商家每天可卖出工艺品![]() 件,若每件工艺品降价
件,若每件工艺品降价![]() 元,则每天可多卖出该工艺品
元,则每天可多卖出该工艺品![]() 件,间每件降价多少元销售,每天获得利润最大?获得最大利润是多少元?
件,间每件降价多少元销售,每天获得利润最大?获得最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与探究
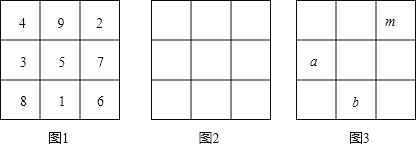
请阅读下列材料,完成相应的任务:幻方:将若干个数组成一个正方形数阵,若任意一行,一列及对角线上的数字之和都相等,则称具有这种性质的数字方阵为“幻方”.中国古代称“幻方”为“河图”“洛书”等,例如,图1是一个三阶幻方,是将数字1,2,3,4,5,6,7,8,9填入到3x3的方格中得到的,其每行、每列、每条对角线上的三个数之和相等,我们称这种幻方为“数字连续型三阶幻方”.
任务:(1)观察图1中三阶幻方中间的数字与9个数的和,可以发现二者有确定的数量关系.设“数字连续型三阶幻方中间的数字是x,幻方中9个数的和为s,则s与x之间的数量关系为 ;
(2)现要用9个数3,4,5,6,7,8,9,10,11构造一个三阶幻方.请将构造的幻方填写在图2的3×3方格中;
(3)某学习小组同学在研究图1的三阶幻方时,发现任何一个角上的数都有两个数与其不在同一行、列及对角线上,并且它们之间存在一个等量关系.为此该小组同学绘制了图3,请你用图3中的字母m,a,b表示他们发现的这个等量关系.(直接写出,不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
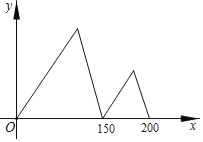
【题目】甲、乙两人在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑步1000米,甲超出乙150米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与乙出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙距离终点还有_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
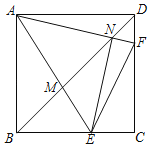
【题目】如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连按EN、EF、有以下结论:①AN=EN,②当AE=AF时,![]() =2﹣
=2﹣![]() ,③BE+DF=EF,④存在点E、F,使得NF>DF,其中正确的个数是( )
,③BE+DF=EF,④存在点E、F,使得NF>DF,其中正确的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
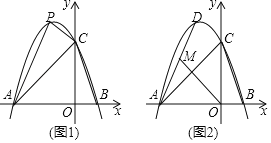
【题目】如图,抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点.
(1)求抛物线的函数表达式;
(2)如图1,P为抛物线上在第二象限内的一点,若△PAC面积为3,求点P的坐标;
(3)如图2,D为抛物线的顶点,在线段AD上是否存在点M,使得以M,A,O为顶点的三角形与△ABC相似?若存在,求点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
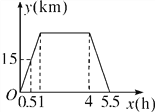
【题目】周末,小李从家里出发骑车到少年宫学习绘画,学完后立即回家,他离家的距离y(km)与时间x(h)之间的函数关系如图所示,有下列结论:①他家离少年宫30km;②他在少年宫一共停留了3h;③他返回家时,离家的距离y(km)与时间x(h)之间的函数表达式是y=-20x+110;④当他离家的距离y=10时,时间x=![]() .其中正确的是________(填序号).
.其中正确的是________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为正方形ABCD的对角线AC上的一点,连接BP并延长交CD于点E,交AD的延长线于点F,⊙O是△DEF的外接圆,连接DP.
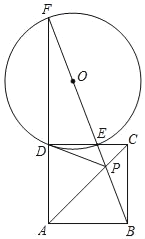
(1)求证:DP是⊙O的切线;
(2)若tan∠PDC=![]() ,正方形ABCD的边长为4,求⊙O的半径和线段OP的长.
,正方形ABCD的边长为4,求⊙O的半径和线段OP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com