
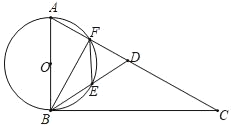
【题目】如图,D为直角△ABC中斜边AC上一点,且AB=AD,以AB为直径的⊙O交AD于点F,交BD于点E,连接BF,BF.
(1)求证:BE=FE;
(2)求证:∠AFE=∠BDC;
(3)已知:sin∠BAE=![]() ,AB=6,求BC的长.
,AB=6,求BC的长.
【答案】(1)见解析;(2)见解析;(3)BC=12![]() .
.
【解析】
(1)连接AE,由AB是直径知AE⊥BD,结合AB=AD知∠BAE=∠DAE,依据∠EBF=∠DAE,∠BFE=∠BAE可得∠EBF=∠BFE,据此即可得证;
(2)由AB=AD知∠ABD=∠2,结合∠1=∠ABD知∠1=∠2,根据∠1+∠AFE=∠2+∠BDC=180°即可得出∠AFE=∠BDC;
(3)作DG⊥BC,由sin∠BAE=![]() ,AB=AD=6知DE=BE=2
,AB=AD=6知DE=BE=2![]() ,BD=4
,BD=4![]() ,再证∠DBG=∠BAE得DG=BDsin∠DBG=4,BG=4
,再证∠DBG=∠BAE得DG=BDsin∠DBG=4,BG=4![]() ,证△CDG∽△CAB得
,证△CDG∽△CAB得![]() =
=![]() ,据此计算可得答案.
,据此计算可得答案.
(1)如图,连接AE,
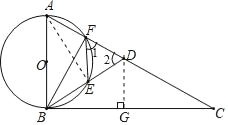
∵AB是圆的直径,
∴∠AEB=90°,即AE⊥BD,
∵AB=AD,
∴∠BAE=∠DAE,
∵∠EBF=∠DAE,∠BFE=∠BAE,
∴∠EBF=∠BFE,
∴BE=EF;
(2)∵AB=AD,
∴∠ABD=∠2,
∵∠1=∠ABD,
∴∠1=∠2,
又∵∠1+∠AFE=∠2+∠BDC=180°,
∴∠AFE=∠BDC;
(3)如图,过点D作DG⊥BC于点G,
∵sin∠BAE=![]() ,AB=AD=6,
,AB=AD=6,
∴DE=BE=2![]() ,
,
∴BD=4![]() ,
,
又∵∠DBG+∠ABD=∠BAE+∠ABD=90°,
∴∠DBG=∠BAE,
∴DG=BDsin∠DBG=4![]() ×
×![]() =4,
=4,
∴BG=4![]() ,
,
∵DG∥AB,
∴△CDG∽△CAB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:BC=12![]() .
.


科目:初中数学 来源: 题型:
【题目】一商家按标价销售工艺品时,每件可获利![]() 元,按标价的八五新销售工艺品
元,按标价的八五新销售工艺品![]() 件与将标价降低
件与将标价降低![]() 元销售这种工艺品
元销售这种工艺品![]() 件所获利润相等.
件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少?
(2)若每件工艺品按此进价进货,标价销售,商家每天可卖出工艺品![]() 件,若每件工艺品降价
件,若每件工艺品降价![]() 元,则每天可多卖出该工艺品
元,则每天可多卖出该工艺品![]() 件,间每件降价多少元销售,每天获得利润最大?获得最大利润是多少元?
件,间每件降价多少元销售,每天获得利润最大?获得最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
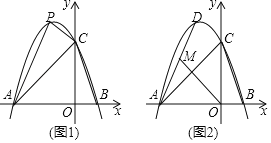
【题目】如图,抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点.
(1)求抛物线的函数表达式;
(2)如图1,P为抛物线上在第二象限内的一点,若△PAC面积为3,求点P的坐标;
(3)如图2,D为抛物线的顶点,在线段AD上是否存在点M,使得以M,A,O为顶点的三角形与△ABC相似?若存在,求点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
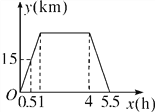
【题目】周末,小李从家里出发骑车到少年宫学习绘画,学完后立即回家,他离家的距离y(km)与时间x(h)之间的函数关系如图所示,有下列结论:①他家离少年宫30km;②他在少年宫一共停留了3h;③他返回家时,离家的距离y(km)与时间x(h)之间的函数表达式是y=-20x+110;④当他离家的距离y=10时,时间x=![]() .其中正确的是________(填序号).
.其中正确的是________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电视节目“奔跑吧兄弟”播出后深受中小学生的喜爱,小刚想知道大家最喜欢哪位“兄弟”,于是在本校随机抽取了一部分学生进行抽查(每人只能选一个自己最喜欢的“兄弟”),将调查结果进行了整理后绘制成如图两幅不完整的统计图,请结合图中提供的信息解答下列问题:

(1)本次被调查的学生有多少人.
(2)将两幅统计图补充完整.
(3)若小刚所在学校有2000名学生,请根据图中信息,估计全校喜欢“Angelababy”的人数.
(4)若从3名喜欢“李晨”的学生和2名喜欢“Angelababy”的学生中随机抽取两人参加文体活动,则两人都是喜欢“李晨”的学生的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”.如20=3+17.
(1)从7、11、19、23这4个素数中随机抽取一个,则抽到的数是7的概率是 ;
(2)从7、11、19、23这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于30的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,对角线为1的正方形OABC,点A在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OBlB2C2,照此规律作下去,则点B2019的坐标为( )
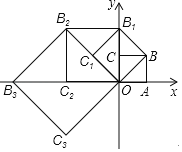
A.(﹣21009,21009)B.(21008,﹣21008)
C.(﹣21009![]() ,0)D.(0,21008
,0)D.(0,21008![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为正方形ABCD的对角线AC上的一点,连接BP并延长交CD于点E,交AD的延长线于点F,⊙O是△DEF的外接圆,连接DP.
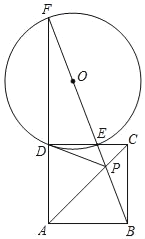
(1)求证:DP是⊙O的切线;
(2)若tan∠PDC=![]() ,正方形ABCD的边长为4,求⊙O的半径和线段OP的长.
,正方形ABCD的边长为4,求⊙O的半径和线段OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B(3,3)在双曲线![]() (x>0)上,点D在双曲线
(x>0)上,点D在双曲线![]() (x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(1)求k的值;
(3)求点A的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com