
【题目】如图,在直角三角形ABC中,直角边![]() ,
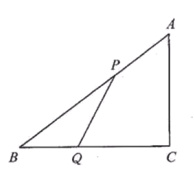
,![]() ,设P、Q分别为AB,BC上的动点,点P自点A沿AB方向向点B作匀速移动且速度为每秒2cm,同时点Q自点B沿BC方向向点C作匀速移动且速度为每秒1cm,当P点到达B点时,Q点就停止移动.设P,Q移动的时间t秒.
,设P、Q分别为AB,BC上的动点,点P自点A沿AB方向向点B作匀速移动且速度为每秒2cm,同时点Q自点B沿BC方向向点C作匀速移动且速度为每秒1cm,当P点到达B点时,Q点就停止移动.设P,Q移动的时间t秒.
(1)写出![]() 的面积S(
的面积S(![]() )与时间t(s)之间的函数表达式,并写出t的取值范围.
)与时间t(s)之间的函数表达式,并写出t的取值范围.
(2)当t为何值时,![]() 为等腰三角形?
为等腰三角形?
【答案】(1)![]() ;(2)当t
;(2)当t![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
【解析】
(1)过点P作PH⊥BC,垂足为H,从而得到△BPH∽△ABC,根据相似比例求出PH的长,然后表示出三角形PBQ的面积即可;
(2)需要分BP=BQ,BQ=PQ和BP=PQ三种情况讨论三角形PBQ为等腰三角形,即最后分别求值即可.
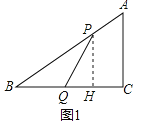
(1)如图1,过点P作PH⊥BC,垂足为H,
∵Rt△ABC中直角边AC=6,BC=8
∴由勾股定理可得AB=10,
∴BP=10-2t,BQ=t.
∵AC⊥C B
∴△BPH∽△ABC,
∴![]() 即
即![]() ,解得
,解得![]() ;
;
∴![]()
(2)①当BP=BQ时,10-2t=t,解得t=![]() 秒;
秒;
②如图2,当BQ=PQ时,作QE⊥BD,垂足为E,
∵BQ=PO,QE⊥BD,
∴![]()
∵∠B=∠B, ∠ACB=∠QEB,
∴△BQE∽△BAC
∴![]() ,即
,即![]() ,即得:t=
,即得:t=![]() 秒;
秒;
③如图3,当BP=PQ时,作PF⊥BC,垂足为F
∵BP=PQ,PF⊥BC,
∴![]()
∵![]()
∴△BPF∽△BAC,
∴![]() ,即:
,即: ,解得:t=
,解得:t=![]() 秒
秒
综上:当![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.


科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,DA为⊙O的切线,切点为A,过⊙O上的点C作CD∥AB交AD于点D,连接BC、AC.
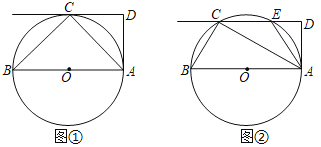
(1)如图①,若DC为⊙O的切线,切点为C,求∠ACD和∠DAC的大小.
(2)如图②,当CD为⊙O的割线且与⊙O交于点E时,连接AE,若∠EAD=30°,求∠ACD和∠DAC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家快递公司揽件员(揽收快件的员工)的日工资方案如下:
甲公司为“基本工资+揽件提成”,其中基本工资为70元/日,每揽收一件提成2元;
乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过40,每件提成4元;若当日搅件数超过40,超过部分每件多提成2元.
如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图:
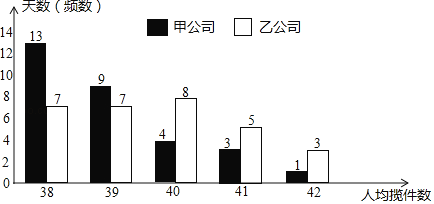
(1)现从今年四月份的30天中随机抽取1天,求这一天甲公司揽件员人均揽件数超过40(不含40)的概率;
(2)根据以上信息,以今年四月份的数据为依据,并将各公司揽件员的人均揽件数视为该公司各揽件员的
揽件数,解决以下问题:
①估计甲公司各揽件员的日平均件数;
②小明拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,井说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,![]() ,
,![]() 的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )

A.17B.18C.19D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 中,
中,![]() ,P是斜边AC上一个动点,以即为直径作
,P是斜边AC上一个动点,以即为直径作![]() 交BC于点D,与AC的另一个交点E,连接DE.
交BC于点D,与AC的另一个交点E,连接DE.
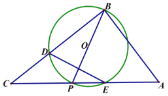
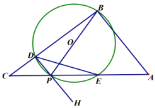
(1)当![]() 时,
时,
①若![]() ,求
,求![]() 的度数;
的度数;
②求证![]() ;
;
(2)当![]() ,
,![]() 时,
时,
①是含存在点P,使得![]() 是等腰三角形,若存在求出所有符合条件的CP的长;
是等腰三角形,若存在求出所有符合条件的CP的长;
②以D为端点过P作射线DH,作点O关于DE的对称点Q恰好落在![]() 内,则CP的取值范围为________.(直接写出结果)
内,则CP的取值范围为________.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点A在函数![]() (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA,交以A为圆心,AB为半径的圆弧于点D;延长BA,交以A为圆心,AC为半径的圆弧于点E.直线DE分别交x,y轴于点P,Q,当QE:DP=4:9时,图中阴影部分的面积等于____.
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA,交以A为圆心,AB为半径的圆弧于点D;延长BA,交以A为圆心,AC为半径的圆弧于点E.直线DE分别交x,y轴于点P,Q,当QE:DP=4:9时,图中阴影部分的面积等于____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示.则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t为实数);⑤点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
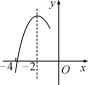
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,若点
中,若点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 和点
和点![]() 关于直线
关于直线![]() 对称,则称点
对称,则称点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点.
的二次对称点.
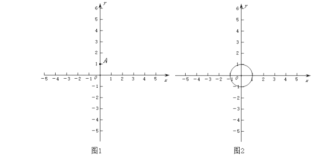
(1)如图1,点![]() .
.
①若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则点
的二次对称点,则点![]() 的坐标为________;
的坐标为________;
②若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则
的二次对称点,则![]() 的值为_______;
的值为_______;
③若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为__________;
的表达式为__________;
(2)如图2,![]() 的半径为1.若
的半径为1.若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直绩
轴,直绩![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在射线
在射线![]() 上,
上,![]() 的取值范围是________;
的取值范围是________;
(3)![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 的半径为2,若
的半径为2,若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在
在![]() 轴上,求
轴上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
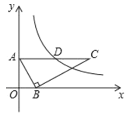
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数(k>0,x>0)的图象经过AC的中点D,则k的值为( )
A.8B.5C.6D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com