
【题目】已知AB是⊙O的直径,DA为⊙O的切线,切点为A,过⊙O上的点C作CD∥AB交AD于点D,连接BC、AC.
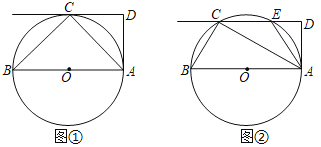
(1)如图①,若DC为⊙O的切线,切点为C,求∠ACD和∠DAC的大小.
(2)如图②,当CD为⊙O的割线且与⊙O交于点E时,连接AE,若∠EAD=30°,求∠ACD和∠DAC的大小.
【答案】(1)∠ACD=∠DAC=45°;(2)∠ACD=30°,∠DAC=60°.
【解析】
(1)先根据题意确定三角形ADC是等腰直角三角形,进而求出∠ACD和∠DAC的大小;
(2)根据AB是圆O的直径,DA为圆O的切线,切点为A,可得DA⊥AB,根据∠EAD=30°,可得∠BAE=60°,根据圆内接四边形对角互补可得∠BCE=120°,根据AB是圆O的直径,可得∠BCA=90°,进而求得∠ACD和∠DAC的大小.
(1)∵AB是⊙O的直径,DA为⊙O的切线,切点为A,
∴DA⊥AB,
∴∠DAB=90°,
∵DC为⊙O的切线,切点为C,
∴DC=DA,
∵CD∥AB,
∴∠D+∠DAB=180°,
∴∠D=90°,
∴∠ACD=∠DAC=45°;
(2)∵AB是⊙O的直径,DA为⊙O的切线,切点为A,
∴DA⊥AB,
∴∠DAB=90°,
∠DEA=∠EAB,
∴∠ADC=90°,
∵∠EAD=30°,
∴∠DEA=60°,
∴∠EAB=60°,
∴∠BCE=120°,
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠ACD=30°,
∴∠DAC=60°.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
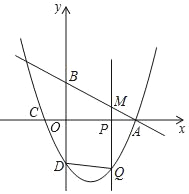
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
(1)求点A的坐标.
(2)求抛物线的表达式.
(3)当以B、D、Q,M为顶点的四边形是平行四边形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,某新建火车站站前广场需要绿化的面积为35000![]() ,施工队在绿化了11000
,施工队在绿化了11000![]() 后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少平方米?
(2)该项绿化工程中有一块长为20![]() 、宽为8
、宽为8![]() 的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56
的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56![]() ,两块绿地之间及周边留有宽度相等的人行通道(如图②所示),则人行通道的宽度是多少米?
,两块绿地之间及周边留有宽度相等的人行通道(如图②所示),则人行通道的宽度是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:抛物线y=a(x+1)(x﹣3)交x轴于A、C两点,交y轴于B.且OB=2CO.
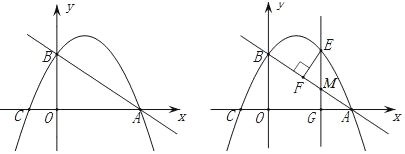
(1)求点A、B、C的坐标及二次函数解析式;
(2)在直线AB上方的抛物线上有动点E,作EG⊥x轴交x轴于点G,交AB于点M,作EF⊥AB于点F.若点M的横坐标为m,求线段EF的最大值.
(3)抛物线对称轴上是否存在点P使得△ABP为直角三角形,若存在请直接写出点P的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
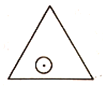
【题目】如图,一个半径为![]() 的圆形纸片在边长为
的圆形纸片在边长为![]() 的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是____________.
的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E为对角线AC上一点,且AE![]() CB,连接DE并延长交BC于点G,过点A作AH⊥BE于点H,交BC于点F.以下结论:①BH
CB,连接DE并延长交BC于点G,过点A作AH⊥BE于点H,交BC于点F.以下结论:①BH![]() HE;②∠BEG
HE;②∠BEG![]() 45°;③△ABF ≌△DCG; ④4BH2
45°;③△ABF ≌△DCG; ④4BH2![]() BG·CD.其中正确结论的个数是( )
BG·CD.其中正确结论的个数是( )
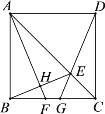
A.1个B.2
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,直角边![]() ,
,![]() ,设P、Q分别为AB,BC上的动点,点P自点A沿AB方向向点B作匀速移动且速度为每秒2cm,同时点Q自点B沿BC方向向点C作匀速移动且速度为每秒1cm,当P点到达B点时,Q点就停止移动.设P,Q移动的时间t秒.
,设P、Q分别为AB,BC上的动点,点P自点A沿AB方向向点B作匀速移动且速度为每秒2cm,同时点Q自点B沿BC方向向点C作匀速移动且速度为每秒1cm,当P点到达B点时,Q点就停止移动.设P,Q移动的时间t秒.
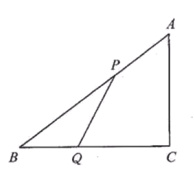
(1)写出![]() 的面积S(
的面积S(![]() )与时间t(s)之间的函数表达式,并写出t的取值范围.
)与时间t(s)之间的函数表达式,并写出t的取值范围.
(2)当t为何值时,![]() 为等腰三角形?
为等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com