
【题目】如图,圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点.则在圆锥的侧面上从B点到P点的最短路线的长为_____.

科目:初中数学 来源: 题型:
【题目】中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题做法全校学生中进行了抽样调查,根据调查结果绘制城如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
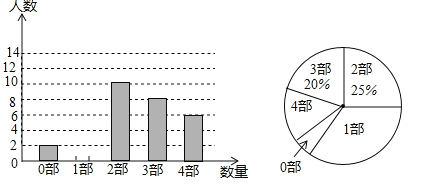
(1)本次调查所得数据的众数是 部,中位数是 部,扇形统计图中“1部”所在扇形的圆心角为 度.
(2)请将条形统计图补充完整;
(3)没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,则他们选中同一名著的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
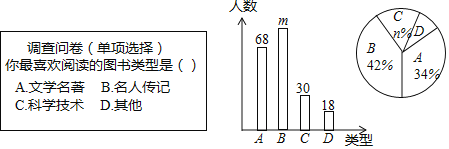
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,DM切⊙O于点D,过点A作AE⊥DM,垂足为E,交⊙O于点C,连接AD.
(1)求证:AD是∠BAC的平分线;
(2)连接CD,若![]() ,半径为5,求CE的长.
,半径为5,求CE的长.
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某县美化城市工程招投标中,有甲、乙两个工程队投标经测算:甲队单独完成这项工程需要30天,若由甲队先做10天,剩下的工程由甲、乙合作12天可完成.问:
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需工程款2万元,该工程计划用时不超过35天,在不超过计划天数的前提下,由甲队先单独施工若干天,剩下的工程由乙队单独完成,那么安排甲队单独施工多少天工程款最省?最省的工程款是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,DA为⊙O的切线,切点为A,过⊙O上的点C作CD∥AB交AD于点D,连接BC、AC.
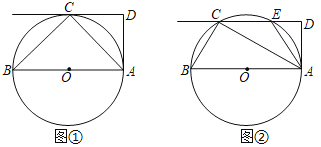
(1)如图①,若DC为⊙O的切线,切点为C,求∠ACD和∠DAC的大小.
(2)如图②,当CD为⊙O的割线且与⊙O交于点E时,连接AE,若∠EAD=30°,求∠ACD和∠DAC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
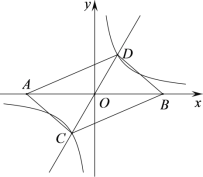
【题目】如图,在平面直角坐标系中,点A的坐标为(m,0),m<0,点B与点A 关于原点对称,直线![]() 与双曲线
与双曲线![]() 交于C,D两点.
交于C,D两点.
(1)直接判断后填空:四边形ACBD的形状一定是 ;
(2)若点D(1,t),求双曲线的解析式;
(3)在(2)的前提下,四边形ACBD为矩形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,![]() ,
,![]() 的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )

A.17B.18C.19D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com