
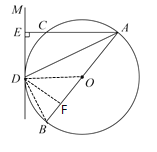
【题目】已知:如图,AB是⊙O的直径,DM切⊙O于点D,过点A作AE⊥DM,垂足为E,交⊙O于点C,连接AD.
(1)求证:AD是∠BAC的平分线;
(2)连接CD,若![]() ,半径为5,求CE的长.
,半径为5,求CE的长.
![]()

【答案】(1)证明见解析;(2)2
【解析】
(1)连接OD,BD,由切线的性质和已知条件易证OD∥AE,再由平行线的性质和圆的半径相等可证∠EAD=∠BAE,即AD是∠BAC的平分线;
(2)过点D作DF⊥AB于点F,由圆周角定理可得CD=DB,再由勾股定理可求出BF的长,易证Rt△CED≌Rt△BFD,由全等三角形的性质可得CE=BF,问题得解.
解:(1)连接OD,BD
∵DM切⊙O于点D,
∴OD⊥MD,
∵AE⊥DM,
∴OD∥AE,
∴∠ODA=∠EAD,
∵OD=OA,
∴∠ODA=∠DAB,
∴∠EAD=∠BAE,
即AD是∠BAC的平分线;
(2)过点D作DF⊥AB于点F,
∵∠EAD=∠BAE,
∴![]() ,
,
∴CD=BD=2![]() ,
,
设BF=x,则OF=5-x,
∴(2![]() )2-x2=52-(5-x)2,
)2-x2=52-(5-x)2,
解得:x=2,
∴BF=2,
在Rt△CED和Rt△BFD中,![]() ,
,
∴Rt△CED≌Rt△BFD(HL),
∴CE=BF=2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,点E为AC延长线上一点,且DE是⊙O的切线.
(1)求证:∠CDE=![]() ∠BAC;
∠BAC;
(2)若AB=3BD,CE=4,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,某新建火车站站前广场需要绿化的面积为35000![]() ,施工队在绿化了11000
,施工队在绿化了11000![]() 后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少平方米?
(2)该项绿化工程中有一块长为20![]() 、宽为8
、宽为8![]() 的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56
的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56![]() ,两块绿地之间及周边留有宽度相等的人行通道(如图②所示),则人行通道的宽度是多少米?
,两块绿地之间及周边留有宽度相等的人行通道(如图②所示),则人行通道的宽度是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF,
(1)求证:AE=CF;
(2)若AB=3,∠AOD=120°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:抛物线y=a(x+1)(x﹣3)交x轴于A、C两点,交y轴于B.且OB=2CO.
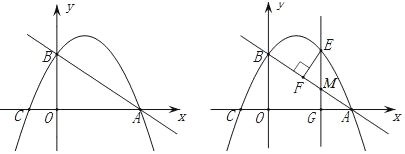
(1)求点A、B、C的坐标及二次函数解析式;
(2)在直线AB上方的抛物线上有动点E,作EG⊥x轴交x轴于点G,交AB于点M,作EF⊥AB于点F.若点M的横坐标为m,求线段EF的最大值.
(3)抛物线对称轴上是否存在点P使得△ABP为直角三角形,若存在请直接写出点P的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E为对角线AC上一点,且AE![]() CB,连接DE并延长交BC于点G,过点A作AH⊥BE于点H,交BC于点F.以下结论:①BH
CB,连接DE并延长交BC于点G,过点A作AH⊥BE于点H,交BC于点F.以下结论:①BH![]() HE;②∠BEG
HE;②∠BEG![]() 45°;③△ABF ≌△DCG; ④4BH2
45°;③△ABF ≌△DCG; ④4BH2![]() BG·CD.其中正确结论的个数是( )
BG·CD.其中正确结论的个数是( )
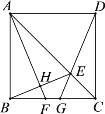
A.1个B.2
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=10,弦BC=![]() ,点P是⊙O上的一动点(不与点A、B重合,且与点C分别位于直径AB的异侧),连接PA,PC,过点C作PC的垂线交PB的延长线于点D.
,点P是⊙O上的一动点(不与点A、B重合,且与点C分别位于直径AB的异侧),连接PA,PC,过点C作PC的垂线交PB的延长线于点D.
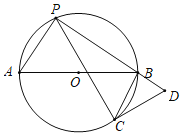
(1)求tan∠BPC的值;
(2)随着点P的运动,![]() 的值是否会发生变化?若变化,请说明理由,若不变,则求出它的值;
的值是否会发生变化?若变化,请说明理由,若不变,则求出它的值;
(3)运动过程中,AP+2BP的最大值是多少?请你直接写出它来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com