
【题目】如图,已知:抛物线y=a(x+1)(x﹣3)交x轴于A、C两点,交y轴于B.且OB=2CO.
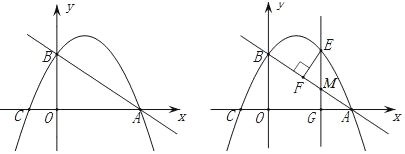
(1)求点A、B、C的坐标及二次函数解析式;
(2)在直线AB上方的抛物线上有动点E,作EG⊥x轴交x轴于点G,交AB于点M,作EF⊥AB于点F.若点M的横坐标为m,求线段EF的最大值.
(3)抛物线对称轴上是否存在点P使得△ABP为直角三角形,若存在请直接写出点P的坐标;若不存在请说明理由.
【答案】(1)y= ![]() ;(2)
;(2)![]() ;(3)点P的坐标为(1,﹣3)或(1,
;(3)点P的坐标为(1,﹣3)或(1,![]() )或(1,1+
)或(1,1+![]() )或(1,1﹣
)或(1,1﹣![]() ),理由见解析
),理由见解析
【解析】
(1)利用待定系数法求出![]() 、
、![]() 、
、![]() 的坐标即可解决问题;
的坐标即可解决问题;
(2)易用![]() 表示线段
表示线段![]() 的长度,再求得
的长度,再求得![]() 和
和![]() 的长度关系,根据等角三角函数或三角形相似即可解题;
的长度关系,根据等角三角函数或三角形相似即可解题;
(3)![]() 为直角三角形时,分别以三个顶点为直角顶点讨论:根据三角形相似和勾股定理列方程解决问题.
为直角三角形时,分别以三个顶点为直角顶点讨论:根据三角形相似和勾股定理列方程解决问题.
(1)对于抛物线y=a(x+1)(x﹣3),令y=0,得到a(x+1)(x﹣3)=0,解得x=﹣1或3,
∴C(﹣1,0),A(3,0),
∴OC=1,
∵OB=2OC=2,
∴B(0,2),
把B(0,2)代入y=a(x+1)(x﹣3)中得:2=﹣3a,![]() ,
,
∴二次函数解析式为![]() ;
;
(2)设直线AB的解析式为:y=kx+b,
把A(3,0),B(0,2)代入得:![]() ,解得:
,解得: ,
,
∴直线AB的解析式为:![]() ,
,
由题意可设![]() ,
,![]() ,
,
则![]() ;
;
∵在Rt△AOB中,根据勾股定理,得![]() ,
,
∵∠EMF+∠FEM=∠AMG+∠BAO=90°,
∵∠AMG=∠EMF,
∴∠FEM=∠BAO,
![]() ,
,
∴ ,
,
∴ ,
,
∴当![]() 时,EF有最大值是
时,EF有最大值是![]() ;
;
(3)∵A(3,0),B(0,2),
∴OA=3,OB=2,
由对称得:抛物线的对称轴是:x=1,
∴AE=3﹣1=2,
设抛物线的对称轴与x轴相交于点E,当△ABP为直角三角形时,存在以下三种情况:
①如图1,当∠BAP=90°时,点P在AB的下方,
∵∠PAE+∠BAO=∠BAO+∠ABO=90°,
∴∠PAE=∠ABO,
∵∠AOB=∠AEP,
∴△ABO∽△PAE,
∴![]() ,即
,即![]() ,
,
∴PE=3,
∴P(1,﹣3);

②如图2,当∠PBA=90°时,点P在AB的上方,过P作PF⊥y轴于F,
同理得:△PFB∽△BOA,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;

③如图3,以AB为直径作圆与对称轴交于P1、P2,则∠AP1B=∠AP2B=90°,
设P1(1,y),
∵AB2=22+32=13,
由勾股定理得:AB2=P1B2+P1A2,
∴12+(y﹣2)2+(3﹣1)2+y2=13,
解得:![]() ,
,
∴![]() 或
或![]() ,
,
综上所述,点P的坐标为(1,﹣3)或(1,![]() )或(1,1+
)或(1,1+![]() )或(1,1﹣
)或(1,1﹣![]() ).
).



科目:初中数学 来源: 题型:
【题目】如图,平行于x轴的直线AC分别交函数 y![]() =x
=x![]() (x≥0)与 y
(x≥0)与 y![]() =
= ![]() x
x![]() (x≥0)的图象于 B,C两点,过点C作y轴的平行线交y
(x≥0)的图象于 B,C两点,过点C作y轴的平行线交y![]() =x
=x![]() (x≥0)的图象于点D,直线DE∥AC交 y
(x≥0)的图象于点D,直线DE∥AC交 y![]() =
=![]() x
x![]() (x≥0)的图象于点E,则
(x≥0)的图象于点E,则![]() =( )
=( )

A. ![]() B. 1 C.
B. 1 C. ![]() D. 3﹣
D. 3﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,E为AB的中点,将△ADE沿DE翻折得到△FDE,延长EF交BC于G, FH⊥BC,垂足为H,连接BF、DG.以下结论:①BF∥ED; ②△DFG ≌△DCG;③△FHB∽△EAD;④tan∠GEB=![]() ;⑤S△BFG=2.4.其中正确的个数是( )
;⑤S△BFG=2.4.其中正确的个数是( )
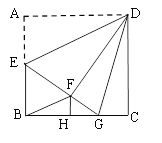
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,DM切⊙O于点D,过点A作AE⊥DM,垂足为E,交⊙O于点C,连接AD.
(1)求证:AD是∠BAC的平分线;
(2)连接CD,若![]() ,半径为5,求CE的长.
,半径为5,求CE的长.
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
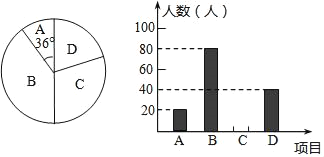
【题目】某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人,在扇形统计图中“D”对应的圆心角的度数为 ;
(2)请你将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,DA为⊙O的切线,切点为A,过⊙O上的点C作CD∥AB交AD于点D,连接BC、AC.
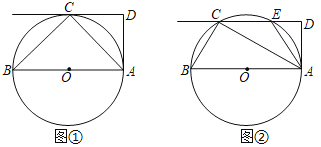
(1)如图①,若DC为⊙O的切线,切点为C,求∠ACD和∠DAC的大小.
(2)如图②,当CD为⊙O的割线且与⊙O交于点E时,连接AE,若∠EAD=30°,求∠ACD和∠DAC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出![]() 关于
关于![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 中,
中,![]() ,P是斜边AC上一个动点,以即为直径作
,P是斜边AC上一个动点,以即为直径作![]() 交BC于点D,与AC的另一个交点E,连接DE.
交BC于点D,与AC的另一个交点E,连接DE.
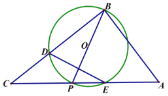
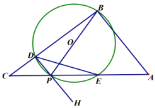
(1)当![]() 时,
时,
①若![]() ,求
,求![]() 的度数;
的度数;
②求证![]() ;
;
(2)当![]() ,
,![]() 时,
时,
①是含存在点P,使得![]() 是等腰三角形,若存在求出所有符合条件的CP的长;
是等腰三角形,若存在求出所有符合条件的CP的长;
②以D为端点过P作射线DH,作点O关于DE的对称点Q恰好落在![]() 内,则CP的取值范围为________.(直接写出结果)
内,则CP的取值范围为________.(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com