
【题目】如图,平行于x轴的直线AC分别交函数 y![]() =x
=x![]() (x≥0)与 y
(x≥0)与 y![]() =
= ![]() x
x![]() (x≥0)的图象于 B,C两点,过点C作y轴的平行线交y
(x≥0)的图象于 B,C两点,过点C作y轴的平行线交y![]() =x
=x![]() (x≥0)的图象于点D,直线DE∥AC交 y
(x≥0)的图象于点D,直线DE∥AC交 y![]() =
=![]() x
x![]() (x≥0)的图象于点E,则
(x≥0)的图象于点E,则![]() =( )
=( )

A. ![]() B. 1 C.
B. 1 C. ![]() D. 3﹣
D. 3﹣ ![]()
科目:初中数学 来源: 题型:
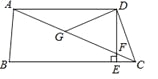
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
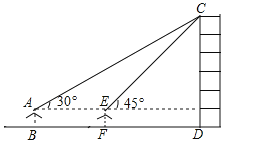
【题目】(7分)小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:![]() ,
,![]() .结果保留整数)
.结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连结CE.

(1)如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE= °.
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由.
②当点D在直线BC上移动时,α,β之间有怎样的数量关系?请你在备用图上画出图形,并直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(2m+1)x+m﹣3;
(1)若函数图象经过原点,求m的值;
(2)若函数图象在y轴的截距为﹣2,求m的值;
(3)若函数的图象平行直线y=3x﹣3,求m的值;
(4)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
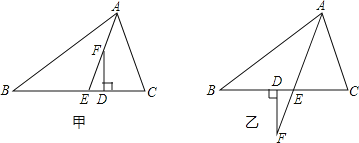
【题目】已知,如图甲,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D.
(1)试说明:∠EFD=![]() (∠C﹣∠B);
(∠C﹣∠B);
(2)当F在AE的延长线上时,如图乙,其余条件不变,(1)中的结论还成立吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com