
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

【答案】已知:①③(或①④或②④或③④),证明见解析.
【解析】试题分析:根据平行四边形的判定方法就可以组合出不同的结论,然后即可证明.
其中解法一是证明两组对角相等的四边形是平行四边形;
解法二是证明两组对边平行的四边形是平行四边形;
解法三是证明一组对边平行且相等的四边形是平行四边形;
解法四是证明两组对角相等的四边形是平行四边形.
试题解析:已知:①③,①④,②④,③④均可,其余均不可以.
解法一:
已知:在四边形ABCD中,①AD∥BC,③∠A=∠C,
求证:四边形ABCD是平行四边形.
证明:∵AD∥BC,
∴∠A+∠B=180°,∠C+∠D=180°.
∵∠A=∠C,
∴∠B=∠D.
∴四边形ABCD是平行四边形.
解法二:
已知:在四边形ABCD中,①AD∥BC,④∠B+∠C=180°,
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,
又∵AD∥BC,
∴四边形ABCD是平行四边形;
解法三:
已知:在四边形ABCD中,②AB=CD,④∠B+∠C=180°,
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD是平行四边形;
解法四:
已知:在四边形ABCD中,③∠A=∠C,④∠B+∠C=180°,
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,
∴∠A+∠D=180°,
又∵∠A=∠C,
∴∠B=∠D,
∴四边形ABCD是平行四边形.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】某采摘农场计划种植A,B两种草莓共6亩,根据表格信息,解答下列问题:
项目 品种 | A | B |
年亩产(单位:千克) | 1200 | 2000 |
采摘价格 | 60 | 40 |
(1)若该农场每年草莓全部被采摘的总收入为460000元,那么A、B两种草莓各种多少亩?
(2)若要求种植A种草莓的亩数不少于种植B种草莓的一半,那么种植A种草莓多少亩时,可使该农场每年草莓全部被采摘的总收入最多?并求出最多总收入.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王红有5张写着以下数字的卡片,请按要求抽出卡片,完成下列各题:![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最小,最小值是 .
(2)从中取出2张卡片,使这2张卡片数字相除商最大,最大值是 .
(3)从中取出除0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能用一次,如:23×[1﹣(﹣2)]),请另写出一种符合要求的运算式子 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了该图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2016次后形成的图形中所有的正方形的面积和是( )

A. 1 B. 2015 C. 201 D. 2017
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
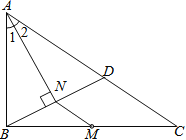
(1)求证:BN=DN;
(2)求△ABC的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y= ![]() x2+1(如图所示).
x2+1(如图所示).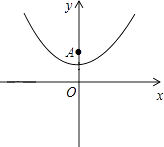
(1)填空:抛物线的顶点坐标是( , ),对称轴是;
(2)已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点N,使四边形OAMN为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
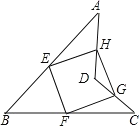
【题目】如图,E. F. G、H分别是边AB、BC、CD、DA的中点.
(1)判断四边形EFGH的形状,并说明你的理由;
(2)连接BD和AC,当BD、AC满足何条件时,四边形EFGH是正方形?证明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com