
【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出![]() 关于
关于![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)当
;(3)当![]() 时,方式一花费少,理由见解析.
时,方式一花费少,理由见解析.
【解析】
(1)根据两种收费方式分别列出等式计算即可;
(2)根据收费方式,方式一分![]() 和
和![]() 两部分,方式二利用“收费
两部分,方式二利用“收费![]() 单次费用
单次费用![]() 次数”即可得;
次数”即可得;
(3)结合题(2)的结论可得当![]() 时,
时,![]() 关于x的函数表达式,再利用一次函数的性质求解即可得.
关于x的函数表达式,再利用一次函数的性质求解即可得.
(1)当![]() 时,方式二收费为
时,方式二收费为![]() (元)
(元)
当![]() 时,方式一收费为
时,方式一收费为![]() (元)
(元)
当![]() 时,方式二收费为
时,方式二收费为![]() (元)
(元)
故答案为:100,250,400;
(2)由题意,当![]() 时,
时,![]()
当![]() 时,
时,![]()
即![]()
当![]() 时,
时,![]()
故![]() 关于x的函数关系式为
关于x的函数关系式为![]() ,
,![]() 关于x的函数关系式为
关于x的函数关系式为![]() ;
;
(3)方式一花费少,理由如下:
由(2)可知,当![]() 时,
时,![]() ,
,![]()
则![]()
记![]()
因为![]()
所以![]() 随
随![]() 的增大而减小
的增大而减小
又![]() 时,
时,![]() ,即
,即![]()
因此,当![]() 时,
时,![]()
故当![]() 时,方式一花费少.
时,方式一花费少.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,点E为AC延长线上一点,且DE是⊙O的切线.
(1)求证:∠CDE=![]() ∠BAC;
∠BAC;
(2)若AB=3BD,CE=4,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:抛物线y=a(x+1)(x﹣3)交x轴于A、C两点,交y轴于B.且OB=2CO.
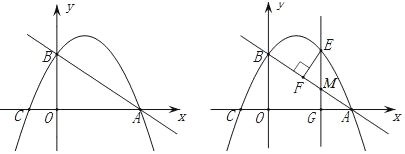
(1)求点A、B、C的坐标及二次函数解析式;
(2)在直线AB上方的抛物线上有动点E,作EG⊥x轴交x轴于点G,交AB于点M,作EF⊥AB于点F.若点M的横坐标为m,求线段EF的最大值.
(3)抛物线对称轴上是否存在点P使得△ABP为直角三角形,若存在请直接写出点P的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E为对角线AC上一点,且AE![]() CB,连接DE并延长交BC于点G,过点A作AH⊥BE于点H,交BC于点F.以下结论:①BH
CB,连接DE并延长交BC于点G,过点A作AH⊥BE于点H,交BC于点F.以下结论:①BH![]() HE;②∠BEG
HE;②∠BEG![]() 45°;③△ABF ≌△DCG; ④4BH2
45°;③△ABF ≌△DCG; ④4BH2![]() BG·CD.其中正确结论的个数是( )
BG·CD.其中正确结论的个数是( )
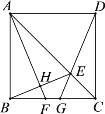
A.1个B.2
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线C1:![]() 与x轴的正半轴交于点A,点B为抛物线的顶点,直线l:
与x轴的正半轴交于点A,点B为抛物线的顶点,直线l:![]() 是一条动直线.
是一条动直线.
(1)求点A、点B的坐标;
(2)当直线l经过点A时,求出直线l的解析式,并直接写出此时当![]() 时,自变量x的取值范围;
时,自变量x的取值范围;
(3)如图2,将抛物线C1在x轴上方的部分沿x轴翻折,与C1在x轴下方的图形组合成一个新的图形C2,当直线l与组合图形C2有且只有两个交点时,直接写出k的取值范围.
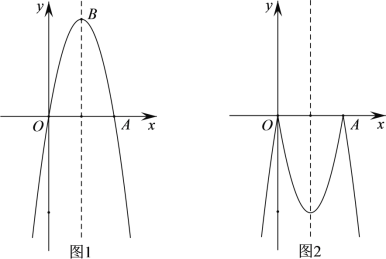
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.
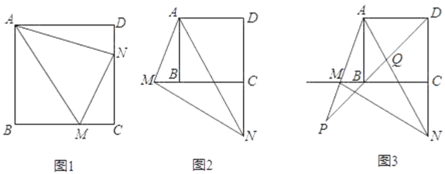
(1)如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;
(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=10,弦BC=![]() ,点P是⊙O上的一动点(不与点A、B重合,且与点C分别位于直径AB的异侧),连接PA,PC,过点C作PC的垂线交PB的延长线于点D.
,点P是⊙O上的一动点(不与点A、B重合,且与点C分别位于直径AB的异侧),连接PA,PC,过点C作PC的垂线交PB的延长线于点D.
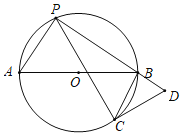
(1)求tan∠BPC的值;
(2)随着点P的运动,![]() 的值是否会发生变化?若变化,请说明理由,若不变,则求出它的值;
的值是否会发生变化?若变化,请说明理由,若不变,则求出它的值;
(3)运动过程中,AP+2BP的最大值是多少?请你直接写出它来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚.对市场最为关注的产量和产量的稳定性进行了抽样调査,过程如下,请补充完整.
收集数据 从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数:
甲 26 32 40 51 44 74 44 63 73 74 81 54 62
41 33 54 43 34 51 63 64 73 64 54 33
乙 27 35 46 55 48 36 47 68 82 48 57 66 75
27 36 57 57 66 58 61 71 38 47 46 71
整理数据 按如下分组整理、描述这两组样本数据:

(说明:45个以下为产量不合格,45个及以上为产量合格,其中45~65个为产量良好,65~85个为产量优秀)分析数据 组样本数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 众数 | 方差 |
甲 | 53 | 54 | 236.24 |
乙 | 53 | 57 | 215.04 |
得出结论 a.估计甲大棚产量良好的秧苗数为________株;b.可以推断出________大棚的小西红柿秧苗品种更适应市场需求,理由为________________.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com