
【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,点E为AC延长线上一点,且DE是⊙O的切线.
(1)求证:∠CDE=![]() ∠BAC;
∠BAC;
(2)若AB=3BD,CE=4,求⊙O的半径.

【答案】(1)见解析;(2)14.
【解析】
(1)根据圆周角定理得出∠ADC=90°,按照等腰三角形的性质和已知的2倍角关系,证明∠ODE为直角即可得到答案;
(2)通过证得△CDE∽△DAE,根据相似三角形的性质即可求得.
(1)如图,连接OD,AD,
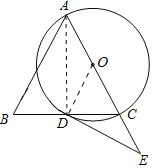
∵AC是直径,
∴∠ADC=90°,-
∴AD⊥BC,
∵AB=AC,
∴∠CAD=∠BAD=![]() ∠BAC,
∠BAC,
∵DE是⊙O的切线;
∴OD⊥DE
∴∠ODE=90°
∴∠ADC=∠ODE
∴∠CDE=∠ADO
∵OA=OD,
∴∠CAD=∠ADO,
∴∠CDE=∠CAD,
![]() ∠CAD=
∠CAD=![]() ∠BAC,
∠BAC,
∴∠CDE=![]() ∠BAC.
∠BAC.

(2)解:∵AB=AC,AD⊥BC,
∴BD=CD,
∵AB=3BD,
∴AC=3DC,
设DC=x,则AC=3x,
∴AD=![]()
∵∠CDE=∠CAD,∠DEC=∠AED,
∴△CDE∽△DAE,
∴![]() ,
,
即![]()
∴DE=![]() ,x=
,x=![]() ,
,
∴AC=3x=28,
∴⊙O的半径为14.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一组数据2,2,3,4,这组数据的中位数是2
B. 了解一批灯泡的使用寿命的情况,适合抽样调查
C. 小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分
D. 某日最高气温是![]() ,最低气温是
,最低气温是![]() ,则该日气温的极差是
,则该日气温的极差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行于x轴的直线AC分别交函数 y![]() =x
=x![]() (x≥0)与 y
(x≥0)与 y![]() =
= ![]() x
x![]() (x≥0)的图象于 B,C两点,过点C作y轴的平行线交y
(x≥0)的图象于 B,C两点,过点C作y轴的平行线交y![]() =x
=x![]() (x≥0)的图象于点D,直线DE∥AC交 y
(x≥0)的图象于点D,直线DE∥AC交 y![]() =
=![]() x
x![]() (x≥0)的图象于点E,则
(x≥0)的图象于点E,则![]() =( )
=( )

A. ![]() B. 1 C.
B. 1 C. ![]() D. 3﹣
D. 3﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李回乡创业,销售一种批发价为4元/千克的水产品.根据市场调查发现,此种水产品的年销售量y(万千克)与售价x(元/千克)之间的关系如图所示:
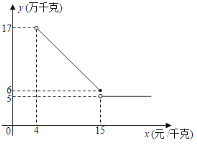
(1)求出销售此种水产品的年销售量y与售价x之间的函数表达式;
(2)市场调查还发现:销售此种水产品需要先投入成本10万元(不含以批发价购入这种水产品所需资金),如果市场管理部门规定此种水产品的销售价不准超过20元/千克,求销售此种水产品售价为多少元时,获得的年利润最大?最大年利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用4000元购进一批某品牌的文化衫若干件,很快售完,该店又用6300元钱购进第二批这种文化衫,所进的件数比第一批多40%,每件文化衫的进价比第一批每件文化衫的进价多10元,请解答下列问题:
(1)求购进的第一批文化衫的件数;
(2)为了取信于顾客,在这两批文化衫的销售中,售价保持了一致.若售完这两批文化衫服装店的总利润不少于4100元钱,那么服装店销售该品牌文化衫每件的最低售价是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,E为AB的中点,将△ADE沿DE翻折得到△FDE,延长EF交BC于G, FH⊥BC,垂足为H,连接BF、DG.以下结论:①BF∥ED; ②△DFG ≌△DCG;③△FHB∽△EAD;④tan∠GEB=![]() ;⑤S△BFG=2.4.其中正确的个数是( )
;⑤S△BFG=2.4.其中正确的个数是( )
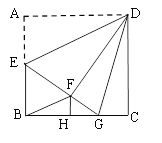
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,DM切⊙O于点D,过点A作AE⊥DM,垂足为E,交⊙O于点C,连接AD.
(1)求证:AD是∠BAC的平分线;
(2)连接CD,若![]() ,半径为5,求CE的长.
,半径为5,求CE的长.
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出![]() 关于
关于![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com