Question

【题目】如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．

（1）求证：CE=CF；

（2）若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？

Answer 1

【答案】（1）见解析（2）成立

【解析】

试题（1）由DF=BE，四边形ABCD为正方形可证△CEB≌△CFD，从而证出CE=CF．

（2）由（1）得，CE=CF，∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可

得∠GCE=∠GCF，故可证得△ECG≌△FCG，即EG=FG=GD+DF．又因为DF=BE，所以可证出GE=BE+GD成立．

试题解析：（1）在正方形ABCD中，

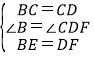
∴△CBE≌△CDF（SAS）．

∴CE=CF．

（2）GE=BE+GD成立．

理由是：∵由（1）得：△CBE≌△CDF，

∴∠BCE=∠DCF，

∴∠BCE+∠ECD=∠DCF+∠ECD，即∠ECF=∠BCD=90°，

又∵∠GCE=45°，∴∠GCF=∠GCE=45°． CE＝CF

∵∠GCE＝∠GCF， GC＝GC

∴△ECG≌△FCG（SAS）．

∴GE=GF．

∴GE=DF+GD=BE+GD．