
【题目】在平面直角坐标系![]() 中,若点
中,若点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 和点
和点![]() 关于直线
关于直线![]() 对称,则称点
对称,则称点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点.
的二次对称点.
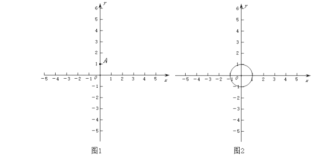
(1)如图1,点![]() .
.
①若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则点
的二次对称点,则点![]() 的坐标为________;
的坐标为________;
②若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则
的二次对称点,则![]() 的值为_______;
的值为_______;
③若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为__________;
的表达式为__________;
(2)如图2,![]() 的半径为1.若
的半径为1.若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直绩
轴,直绩![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在射线
在射线![]() 上,
上,![]() 的取值范围是________;
的取值范围是________;
(3)![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 的半径为2,若
的半径为2,若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在
在![]() 轴上,求
轴上,求![]() 的取值范围.
的取值范围.
【答案】(1)①(4,-1);②2;③y=-x+1;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)数形结合方法,直接结合图形求出即可;
(2)当M(-1,0)时,可求得b的最小值为![]() ,当点
,当点![]() 时,可求得b的最大值为
时,可求得b的最大值为![]() ;
;
(3)确定t取最大值或最小值时,唯一对称点的位置,反过来计算即可.
(1)如图1,
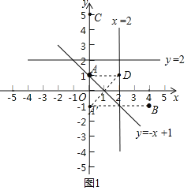
①∵A(0,1);
∴点A关于x轴的对称点A′(0,-1),点A′(0,-1)关于直线l1:x=2的对称点为B(4,-1),
故答案为:(4,-1),
②∵A(0,1),
∴点A关于x轴的对称点A′(0,-1),点A′(0,-1)关于直线l2:y=2的对称点为C(0,5),
故答案为:2,
③∵点A关于x轴的对称点A′(0,-1),点A′(0,-1)与点D(2,1)关于直线l3对称,连接A′D,
∴直线l3⊥A′D,且平分A′D,易求得A′D的中点坐标为(1,0),易知:AD=AA′,
∴经过(0,1),(1,0)两点的直线即为直线l3,
∴y=-x+1;
故答案为:y=-x+1;
(2)如图2,
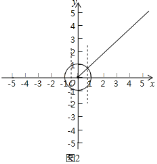
当M(-1,0)时,可求得b的最小值为![]() ,
,
当点![]() 时,可求得b的最大值为
时,可求得b的最大值为![]() ,
,
∴![]() ,
,
故答案为:![]() ;
;
(3)∵E(0,t)为⊙E的圆心,半径为2,过点E作EN′⊥l5交x轴于点N′,
设直线l5: ![]() 与x轴交点为M,则
与x轴交点为M,则![]() ,当t取最大值时,依题意有:
,当t取最大值时,依题意有:
![]() ,
,
解得: ![]()
设⊙E与y轴交点中最上方点为P,过P作PN″⊥l5交x轴于点N″,当t取最小值时有:
![]() ,
,
解得:t=1
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,直角边![]() ,
,![]() ,设P、Q分别为AB,BC上的动点,点P自点A沿AB方向向点B作匀速移动且速度为每秒2cm,同时点Q自点B沿BC方向向点C作匀速移动且速度为每秒1cm,当P点到达B点时,Q点就停止移动.设P,Q移动的时间t秒.
,设P、Q分别为AB,BC上的动点,点P自点A沿AB方向向点B作匀速移动且速度为每秒2cm,同时点Q自点B沿BC方向向点C作匀速移动且速度为每秒1cm,当P点到达B点时,Q点就停止移动.设P,Q移动的时间t秒.
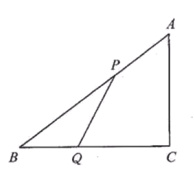
(1)写出![]() 的面积S(
的面积S(![]() )与时间t(s)之间的函数表达式,并写出t的取值范围.
)与时间t(s)之间的函数表达式,并写出t的取值范围.
(2)当t为何值时,![]() 为等腰三角形?
为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D.过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
(1)求证:BC是⊙O的切线;
(2)若AC=6,BC=8,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚.对市场最为关注的产量和产量的稳定性进行了抽样调査,过程如下,请补充完整.
收集数据 从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数:
甲 26 32 40 51 44 74 44 63 73 74 81 54 62
41 33 54 43 34 51 63 64 73 64 54 33
乙 27 35 46 55 48 36 47 68 82 48 57 66 75
27 36 57 57 66 58 61 71 38 47 46 71
整理数据 按如下分组整理、描述这两组样本数据:

(说明:45个以下为产量不合格,45个及以上为产量合格,其中45~65个为产量良好,65~85个为产量优秀)分析数据 组样本数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 众数 | 方差 |
甲 | 53 | 54 | 236.24 |
乙 | 53 | 57 | 215.04 |
得出结论 a.估计甲大棚产量良好的秧苗数为________株;b.可以推断出________大棚的小西红柿秧苗品种更适应市场需求,理由为________________.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚.对于市场最为关注的产量和产量的稳定性,进行了抽样调查,过程如下,请补充完整.
收集数据 从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数:
甲 26 32 40 51 44 74 44 63 73 74 81 54 62 41 33 54 43 34 51 63 64 73 64 54 33
乙 27 35 46 55 48 36 47 68 82 48 57 66 75 27 36 57 57 66 58 61 71 38 47 46 71
整理、描述数据 按如下分组整理、描述这两组样本数据
个数 株数 大棚 |
|
|
|
|
|
|
甲 | 5 | 5 | 5 | 5 | 4 | 1 |
乙 | 2 | 4 | 6 | 2 |
(说明:45个以下为产量不合格,45个及以上为产量合格,其中45~65个为产量良好,65~85个为产量优秀)
分析数据 两组样本数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 众数 | 方差 |
甲 | 53 | 54 | 3047 |
乙 | 53 | 57 | 3022 |
得出结论:(1)估计乙大棚产量优秀的秧苗数为__________株;
(2)可以推断出__________大棚的小西红柿秧苗品种更适应市场需求,理由为_____________________.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个三角形绕其中一个顶点逆时针旋转并放大或缩小(这个顶点不变),我们把这样的三角形
运动称为三角形的T-变换,这个顶点称为T-变换中心,旋转角称为T-变换角,三角形与原三角形的对应边
之比称为T-变换比;已知△![]() 在直角坐标平面内,点
在直角坐标平面内,点![]() ,
,![]() ,
,![]() ,将△
,将△![]() 进
进
行T-变换,T-变换中心为点![]() ,T-变换角为60°,T-变换比为
,T-变换角为60°,T-变换比为![]() ,那么经过T-变换后点
,那么经过T-变换后点![]() 所对应的点的
所对应的点的
坐标为 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
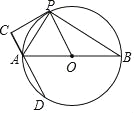
【题目】如图,已知AB是⊙O的直径,PC切⊙O于点P,过A作直线AC⊥PC交⊙O于另一点D,连接PA、PB.
(1)求证:AP平分∠CAB;
(2)若P是直径AB上方半圆弧上一动点,⊙O的半径为2,则
①当弦AP的长是_____时,以A,O,P,C为顶点的四边形是正方形;
②当![]() 的长度是______时,以A,D,O,P为顶点的四边形是菱形.
的长度是______时,以A,D,O,P为顶点的四边形是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com