
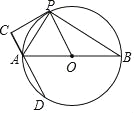
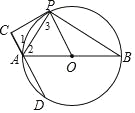
【题目】如图,已知AB是⊙O的直径,PC切⊙O于点P,过A作直线AC⊥PC交⊙O于另一点D,连接PA、PB.
(1)求证:AP平分∠CAB;
(2)若P是直径AB上方半圆弧上一动点,⊙O的半径为2,则
①当弦AP的长是_____时,以A,O,P,C为顶点的四边形是正方形;
②当![]() 的长度是______时,以A,D,O,P为顶点的四边形是菱形.
的长度是______时,以A,D,O,P为顶点的四边形是菱形.
【答案】(1)证明见解析;(2)①2![]() ;②
;②![]() π或
π或![]() π.
π.
【解析】
(1)利用切线的性质得OP⊥PC,再证明AC∥OP得到∠1=∠3,加上∠2=∠3,所以∠1=∠2;
(2)①当∠AOP=90°,根据正方形的判定方法得到四边形AOPC为正方形,从而得到AP=2![]() ;
;
②根据菱形的判定方法,当AD=AP=OP=OD时,四边形ADOP为菱形,所以△AOP和△AOD为等边三角形,然后根据弧长公式计算![]() 的长度.当AD=DP=PO=OA时,四边形ADPO为菱形,△AOD和△DOP为等边三角形,则∠AOP=120°,根据弧长公式计算
的长度.当AD=DP=PO=OA时,四边形ADPO为菱形,△AOD和△DOP为等边三角形,则∠AOP=120°,根据弧长公式计算![]() 的长度.
的长度.
(1)∵PC切⊙O于点P,
∴OP⊥PC,
∵AC⊥PC,
∴AC∥OP,
∴∠1=∠3,
∵OP=OA,
∴∠2=∠3,
∴∠1=∠2,
∴AP平分∠CAB;
(2)①当∠AOP=90°,四边形AOPC为矩形,而OA=OP,此时矩形AOPC为正方形,
AP=![]() OP=2
OP=2![]() ;
;
②当AD=AP=OP=OD时,四边形ADOP为菱形,△AOP和△AOD为等边三角形,则∠AOP=60°,![]() 的长度=
的长度=![]() =
=![]() π.
π.
当AD=DP=PO=OA时,四边形ADPO为菱形,△AOD和△DOP为等边三角形,则∠AOP=120°,![]() 的长度=
的长度=![]() .
.
故答案为2![]() ;
;![]() π或
π或![]() π.
π.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
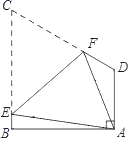
【题目】如图,在四边形ABCD中,∠A=∠B=90°,∠C=60°,BC=CD=8,将四边形ABCD折叠,使点C与点A重合,折痕为EF,则BE的长为( )
A. 1B. 2C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
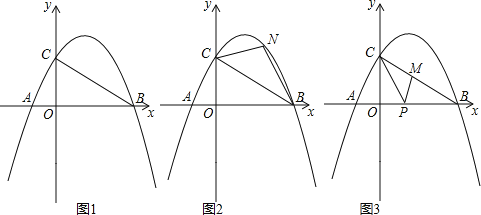
【题目】如图,抛物线y=-![]() [(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
[(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
(2)如图,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
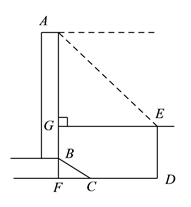
【题目】如图所示,某办公大楼正前方有一根高度是![]() 米的旗杆
米的旗杆![]() ,从办公楼顶端
,从办公楼顶端![]() 测得旗杆顶端
测得旗杆顶端![]() 的俯角
的俯角![]() 是
是![]() ,旗杆底端
,旗杆底端![]() 到大楼前梯坎底边的距离
到大楼前梯坎底边的距离![]() 是
是![]() 米,梯坎坡长
米,梯坎坡长![]() 是
是![]() 米,梯坎坡度
米,梯坎坡度![]() ,求大楼
,求大楼![]() 的高度.(精确到
的高度.(精确到![]() 米,参与数据:
米,参与数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2﹣
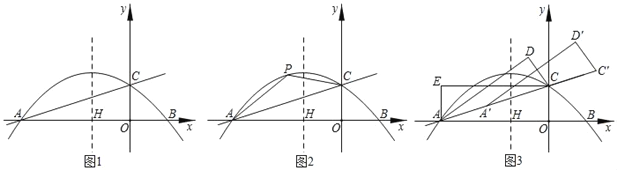
x2﹣![]() x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
(1)求直线AC的解析式;
(2)如图2,P为直线AC上方抛物线上的任意一点,在对称轴上有一动点M,当四边形AOCP面积最大时,求|PM﹣OM|的最大值.
(3)如图3,将△AOC沿直线AC翻折得△ACD,再将△ACD沿着直线AC平移得△A'C′D'.使得点A′、C'在直线AC上,是否存在这样的点D′,使得△A′ED′为直角三角形?若存在,请求出点D′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
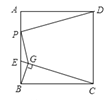
【题目】如图,已知正方形ABCD的边长是4,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
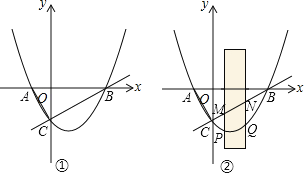
【题目】如图①,直线y=![]() 与x轴、y轴分别交于点B,C,抛物线y=
与x轴、y轴分别交于点B,C,抛物线y=![]() 过B,C两点,且与x轴的另一个交点为点A,连接AC.
过B,C两点,且与x轴的另一个交点为点A,连接AC.
(1)求抛物线的解析式;
(2)在抛物线上是否存在点D(与点A不重合),使得S△DBC=S△ABC,若存在,求出点D的坐标;若不存在,请说明理由;
(3)有宽度为2,长度足够长的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线CB于点M和点N,在矩形平移过程中,当以点P,Q,M,N为顶点的四边形是平行四边形时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
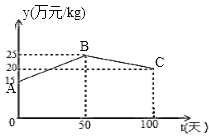
【题目】经过市场调查得知,某种商品的销售期为100天,设该商品销量单价为y(万元/kg),y与时间t(天)函数关系如下图所示,其中线段AB表示前50天销售单价y(万元/kg)与时间t(天)的函数关系;线段BC的函数关系式为y=-![]() t+m.该商品在销售期内的销量如下表:
t+m.该商品在销售期内的销量如下表:
时间t(天) | 0<t≤50 | 50<t≤100 |
销量(kg) | 200 |
|
(1)分别求出当0<t≤50和50<t≤100时y与t的函数关系式;
(2)设每天的销售收入为w(万元),则当t为何值时,w的值最大?求出最大值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享单车为大众出行提供了方便,如图为单车实物图,如图为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知,∠ABE=70°,∠EAB=45°,车轮半径为0.3m,BE=0.4m.小明体验后觉得当坐垫C离地面高度为0.9m时骑着比较舒适,求此时CE的长.(结果精确到1cm)参考数据:sin70.≈0.94,cos70.≈0.34,tan70.≈2.75,![]() ≈1.41
≈1.41

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com