
ĄŸÌâÄżĄżÒŃÖȘĆŚÎïÏßyŁœ©![]() x2©
x2©![]() x+2ÓëxÖ᜻ÓÚ”ăAŁŹBÁœ”㣏œ»yÖáÓÚC”㣏ƌÎïÏߔĶԳÆÖáÓëxÖ᜻ÓÚH”㣏·Ö±đÒÔOCĄąOAÎȘ±ßŚśŸŰĐÎAECOŁź
x+2ÓëxÖ᜻ÓÚ”ăAŁŹBÁœ”㣏œ»yÖáÓÚC”㣏ƌÎïÏߔĶԳÆÖáÓëxÖ᜻ÓÚH”㣏·Ö±đÒÔOCĄąOAÎȘ±ßŚśŸŰĐÎAECOŁź
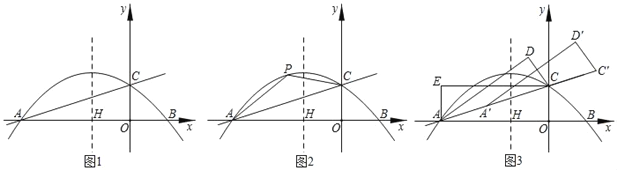
Łš1Ł©ÇóÖ±ÏßAC”ÄœâÎöÊœŁ»
Łš2Ł©ÈçÍŒ2ŁŹPÎȘÖ±ÏßACÉÏ·œĆŚÎïÏßÉÏ”ÄÈÎÒâÒ»”㣏ÔÚ¶ÔłÆÖáÉÏÓĐÒ»¶Ż”ăMŁŹ”±ËıßĐÎAOCPĂæ»ęŚîŽóʱŁŹÇó|PM©OM|”ÄŚîŽóÖ”Łź
Łš3Ł©ÈçÍŒ3ŁŹœ«ĄśAOCŃŰÖ±ÏßAC·ŐÛ”ĂĄśACDŁŹÔÙœ«ĄśACDŃŰŚĆÖ±ÏßACÆœÒÆ”ĂĄśA'CĄäD'ŁźÊč”Ă”ăAĄäĄąC'ÔÚÖ±ÏßACÉÏŁŹÊÇ·ńŽæÔÚŐâŃù”Ä”ăDĄäŁŹÊč”ĂĄśAĄäEDĄäÎȘÖ±œÇÈęœÇĐÎŁżÈôŽæÔÚŁŹÇëÇółö”ăDĄä”ÄŚű±êŁ»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁź
ĄŸŽđ°žĄż(1) yŁœ![]() x+2Ł»(2) ”ăMŚű±êÎȘŁš©2ŁŹ
x+2Ł»(2) ”ăMŚű±êÎȘŁš©2ŁŹ![]() Ł©Ê±ŁŹËıßĐÎAOCP”ÄĂæ»ęŚîŽóŁŹŽËʱ|PM©OM|ÓĐŚîŽóÖ”
Ł©Ê±ŁŹËıßĐÎAOCP”ÄĂæ»ęŚîŽóŁŹŽËʱ|PM©OM|ÓĐŚîŽóÖ”![]() Ł» (3)ŽæÔÚŁŹDĄäŚű±êÎȘŁșŁš0ŁŹ4Ł©»òŁš©6ŁŹ2Ł©»òŁš
Ł» (3)ŽæÔÚŁŹDĄäŚű±êÎȘŁșŁš0ŁŹ4Ł©»òŁš©6ŁŹ2Ł©»òŁš![]() ŁŹ
ŁŹ![]() Ł©Łź
Ł©Łź
ĄŸœâÎöĄż
Łš1Ł©ÁîxŁœ0ŁŹÔòyŁœ2ŁŹÁîyŁœ0ŁŹÔòxŁœ2»ò©6ŁŹÇółö”ăAĄąBĄąCŚű±êŁŹŒŽżÉÇóœâŁ»
Łš2Ł©ÁŹœÓOPœ»¶ÔłÆÖáÓÚ”ăMŁŹŽËʱŁŹ|PM©OM|ÓĐŚîŽóÖ”ŁŹŒŽżÉÇóœâŁ»
Łš3Ł©ŽæÔÚŁ»·ÖąÙAĄäDĄäĄÍAĄäEŁ»ąÚAĄäDĄäĄÍEDĄäŁ»ąÛEDĄäĄÍAĄäEÈęÖÖÇéżöÀûÓĂčŽčɶšÀíÁĐ·œłÌÇóœâŒŽżÉŁź
Łš1Ł©ÁîxŁœ0ŁŹÔòyŁœ2ŁŹÁîyŁœ0ŁŹÔòxŁœ2»ò©6ŁŹĄàAŁš©6ŁŹ0Ł©ĄąBŁš2ŁŹ0Ł©ĄąCŁš0ŁŹ2Ł©ŁŹșŻÊę¶ÔłÆÖáÎȘŁșxŁœ©2ŁŹ¶„”ăŚű±êÎȘŁš©2ŁŹ![]() Ł©ŁŹC”ăŚű±êÎȘŁš0ŁŹ2Ł©ŁŹÔòčę”ăC”ÄÖ±Ïß±íŽïÊœÎȘŁșyŁœkx+2ŁŹœ«”ăAŚű±êŽúÈëÉÏÊœŁŹœâ”ĂŁșk
Ł©ŁŹC”ăŚű±êÎȘŁš0ŁŹ2Ł©ŁŹÔòčę”ăC”ÄÖ±Ïß±íŽïÊœÎȘŁșyŁœkx+2ŁŹœ«”ăAŚű±êŽúÈëÉÏÊœŁŹœâ”ĂŁșk![]() ŁŹÔòŁșÖ±ÏßAC”ıíŽïÊœÎȘŁșy
ŁŹÔòŁșÖ±ÏßAC”ıíŽïÊœÎȘŁșy![]() x+2Ł»
x+2Ł»
Łš2Ł©ÈçÍŒŁŹčę”ăPŚśxÖá”ÄŽčÏßœ»ACÓÚ”ăHŁź
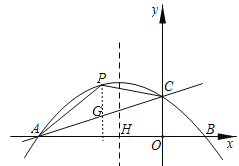
ËıßĐÎAOCPĂæ»ęŁœĄśAOC”ÄĂæ»ę+ĄśACP”ÄĂæ»ęŁŹËıßĐÎAOCPĂæ»ęŚîŽóʱŁŹÖ»ĐèÒȘĄśACP”ÄĂæ»ęŚîŽóŒŽżÉŁŹÉè”ăPŚű±êÎȘŁšmŁŹ![]() m2
m2![]() m+2Ł©ŁŹÔò”ăGŚű±êÎȘŁšmŁŹ
m+2Ł©ŁŹÔò”ăGŚű±êÎȘŁšmŁŹ![]() m+2Ł©ŁŹSĄśACP
m+2Ł©ŁŹSĄśACP![]() PGOA
PGOA![]() Łš
Łš![]() m2
m2![]() m+2
m+2![]() m©2Ł©6
m©2Ł©6![]() m2©3mŁŹ”±mŁœ©3ʱŁŹÉÏÊœÈĄ”ĂŚîŽóÖ”ŁŹÔò”ăPŚű±êÎȘŁš©3ŁŹ
m2©3mŁŹ”±mŁœ©3ʱŁŹÉÏÊœÈĄ”ĂŚîŽóÖ”ŁŹÔò”ăPŚű±êÎȘŁš©3ŁŹ![]() Ł©ŁźÁŹœÓOPœ»¶ÔłÆÖáÓÚ”ăMŁŹŽËʱŁŹ|PM©OM|ÓĐŚîŽóÖ”ŁŹÖ±ÏßOP”ıíŽïÊœÎȘŁșy
Ł©ŁźÁŹœÓOPœ»¶ÔłÆÖáÓÚ”ăMŁŹŽËʱŁŹ|PM©OM|ÓĐŚîŽóÖ”ŁŹÖ±ÏßOP”ıíŽïÊœÎȘŁșy![]() xŁŹ”±xŁœ©2ʱŁŹy
xŁŹ”±xŁœ©2ʱŁŹy![]() ŁŹŒŽŁș”ăMŚű±êÎȘŁš©2ŁŹ
ŁŹŒŽŁș”ăMŚű±êÎȘŁš©2ŁŹ![]() Ł©ŁŹ|PM©OM|”ÄŚîŽóÖ”ÎȘŁș
Ł©ŁŹ|PM©OM|”ÄŚîŽóÖ”ÎȘŁș![]() =
=![]() Łź
Łź
Łš3Ł©ŽæÔÚŁź
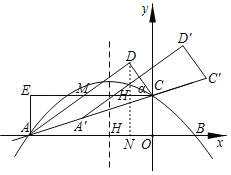
ĄßAEŁœCDŁŹĄÏAECŁœĄÏADCŁœ90ĄăŁŹĄÏEMAŁœĄÏDMCŁŹĄàĄśEAMĄŐĄśDCMŁšAASŁ©ŁŹĄàEMŁœDMŁŹAMŁœMCŁŹÉèŁșEMŁœaŁŹÔòŁșMCŁœ6©aŁźÔÚRtĄśDCMÖĐŁŹÓÉčŽčɶšÀí”ĂŁșMC2ŁœDC2+MD2ŁŹŒŽŁșŁš6©aŁ©2Łœ22+a2ŁŹœâ”ĂŁșa![]() ŁŹÔòŁșMC
ŁŹÔòŁșMC![]() ŁŹčę”ăDŚśxÖá”ÄŽčÏßœ»xÖáÓÚ”ăNŁŹœ»ECÓÚ”ăHŁźÔÚRtĄśDMCÖĐŁŹ
ŁŹčę”ăDŚśxÖá”ÄŽčÏßœ»xÖáÓÚ”ăNŁŹœ»ECÓÚ”ăHŁźÔÚRtĄśDMCÖĐŁŹ![]() DHMC
DHMC![]() MDDCŁŹŒŽŁșDH
MDDCŁŹŒŽŁșDH![]() 2ŁŹÔòŁșDH
2ŁŹÔòŁșDH![]() ŁŹHC
ŁŹHC![]() ŁŹŒŽŁș”ăD”ÄŚű±êÎȘŁš
ŁŹŒŽŁș”ăD”ÄŚű±êÎȘŁš![]() Ł©Ł»
Ł©Ł»
ÉèŁșĄśACDŃŰŚĆÖ±ÏßACÆœÒÆÁËmžö”„λŁŹÔòŁș”ăAĄäŚű±êŁš©6![]() Ł©ŁŹ”ăDĄäŚű±êÎȘŁš
Ł©ŁŹ”ăDĄäŚű±êÎȘŁš![]() Ł©ŁŹ¶ű”ăEŚű±êÎȘŁš©6ŁŹ2Ł©ŁŹÔò
Ł©ŁŹ¶ű”ăEŚű±êÎȘŁš©6ŁŹ2Ł©ŁŹÔò![]() =
=![]() =36ŁŹ
=36ŁŹ![]() =
=![]() =
=![]() ŁŹ
ŁŹ![]() =
=![]() =
=![]() ŁźÈôĄśAĄäEDĄäÎȘÖ±œÇÈęœÇĐÎŁŹ·ÖÈęÖÖÇéżöÌÖÂÛŁș
ŁźÈôĄśAĄäEDĄäÎȘÖ±œÇÈęœÇĐÎŁŹ·ÖÈęÖÖÇéżöÌÖÂÛŁș
ąÙ”±![]() +
+![]() =
=![]() ʱŁŹ36+
ʱŁŹ36+![]() =
=![]() ŁŹœâ”ĂŁșm=
ŁŹœâ”ĂŁșm=![]() ŁŹŽËʱDĄäŁš
ŁŹŽËʱDĄäŁš![]() Ł©ÎȘŁš0ŁŹ4Ł©Ł»
Ł©ÎȘŁš0ŁŹ4Ł©Ł»
ąÚ”±![]() +
+![]() =
=![]() ʱŁŹ36+
ʱŁŹ36+![]() =
=![]() ŁŹœâ”ĂŁșm=
ŁŹœâ”ĂŁșm=![]() ŁŹŽËʱDĄäŁš
ŁŹŽËʱDĄäŁš![]() Ł©ÎȘŁšŁ6ŁŹ2Ł©Ł»
Ł©ÎȘŁšŁ6ŁŹ2Ł©Ł»
ąÛ”±![]() +
+![]() =
=![]() ʱŁŹ
ʱŁŹ![]() +
+![]() =36ŁŹœâ”ĂŁșm=
=36ŁŹœâ”ĂŁșm=![]() »òm=
»òm=![]() ŁŹŽËʱDĄäŁš
ŁŹŽËʱDĄäŁš![]() Ł©ÎȘŁšŁ6ŁŹ2Ł©»òŁš
Ł©ÎȘŁšŁ6ŁŹ2Ł©»òŁš![]() ŁŹ
ŁŹ![]() Ł©Łź
Ł©Łź
ŚÛÉÏËùÊöŁșDŚű±êÎȘŁșŁš0ŁŹ4Ł©»òŁš©6ŁŹ2Ł©»òŁš![]() ŁŹ
ŁŹ![]() Ł©Łź
Ł©Łź


 ÆßĐÇÍŒÊéżÚËăËÙËăÌìÌìÁ·Ï”ÁĐŽđ°ž
ÆßĐÇÍŒÊéżÚËăËÙËăÌìÌìÁ·Ï”ÁĐŽđ°ž łőÖĐŃ§Ò”żŒÊÔ”ŒÓëÁ·Ï”ÁĐŽđ°ž
łőÖĐŃ§Ò”żŒÊÔ”ŒÓëÁ·Ï”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒ,ÒŃÖȘ![]() Ą
Ą![]() ÊÇ
ÊÇ![]() ÖáÉÏ”Ä”ăŁŹÇÒ
ÖáÉÏ”Ä”ăŁŹÇÒ![]() Ą
Ą![]() ŁŹ·Ö±đčę”ă
ŁŹ·Ö±đčę”ă![]() Ą
Ą![]() Śś
Śś![]() Öá”ÄŽčÏßœ»·Ž±ÈÀęșŻÊę
Öá”ÄŽčÏßœ»·Ž±ÈÀęșŻÊę![]() ”ÄÍŒÏóÓÚ”ă
”ÄÍŒÏóÓÚ”ă![]() Ą
Ą![]() ,čę”ă
,čę”ă![]() Śś
Śś![]() ÓÚ”ă
ÓÚ”ă![]() ,čę”ă
,čę”ă![]() Śś
Śś![]() ÓÚ”ă
ÓÚ”ă![]() ĄĄŒÇ
ĄĄŒÇ![]() ”ÄĂæ»ęÎȘ
”ÄĂæ»ęÎȘ![]() ,
,![]() ”ÄĂæ»ęÎȘ
”ÄĂæ»ęÎȘ![]() ĄĄ
ĄĄ![]() ”ÄĂæ»ęÎȘ
”ÄĂæ»ęÎȘ![]() ŁŹÔò
ŁŹÔò![]() Ą
Ą![]() ”ÈÓÚ_________Łź
”ÈÓÚ_________Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
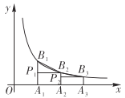
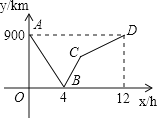
ĄŸÌâÄżĄżÒ»ÁĐżìł”ŽÓŒŚ”ŰÊ»ÍùÒÒ”ŰŁŹÒ»ÁĐÂęł”ŽÓÒÒ”ŰÊ»ÍùŒŚ”ŰŁŹÁœł”ÍŹÊ±łö·ąŁŹÉèÂęł”ĐĐÊ»”ÄʱŒäÎȘxŁšhŁ©ŁŹÁœł”ÖźŒä”ÄŸàÀëÎȘyŁškmŁ©ŁŹÍŒÖĐ”ÄŐÛÏß±íÊŸyÓëxÖźŒä”ÄșŻÊęčŰÏ”ŁźÈô”Ú¶țÁĐżìł”ÒČŽÓŒŚ”Űłö·ąÊ»ÍùÒÒ”ŰŁŹËÙ¶ÈÓë”ÚÒ»ÁĐżìł”ÏàÍŹŁźÔÚ”ÚÒ»ÁĐżìł”ÓëÂęł”ÏàÓö0.5ĐĄÊ±ș󣏔ڶțÁĐżìł”ÓëÂęł”ÏàÓöŁźÔò”Ú¶țÁĐżìł”±È”ÚÒ»ÁĐżìł”Ííłö·ą__ĐĄÊ±.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżĄ°ČĆÒûł€ÉłËźŁŹÓÖÊłÎäČęÓ㥱.ÒòÒ»ŽúΰÈËĂ«Ôó¶«”ÄŒŃŸäŁŹĄ°¶őÖĘÎäČęÓ㥱ĂûŃïÌìÏÂ.ÄłÍű”êŚšĂĆÏúÊÛÄłÖÖÆ·ĆÆŐæżŐ°üŚ°”ÄÎäČęÓăÊìÊłČúÆ·ŁŹłÉ±ŸÎȘ30ÔȘ/șĐŁŹĂżÌìÏúÊÛy(șĐ)ÓëÏúÊÛ”„ŒÛx(ÔȘ)ÖźŒäŽæÔÚÒ»ŽÎșŻÊęčŰÏ”ŁŹÈçÍŒËùÊŸŁź
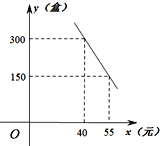
(1)ÇóyÓëxÖźŒä”ÄșŻÊęčŰϔʜŁ»
(2)Èçčûčæ¶šĂżÌìŐâÖÖÎäČęÓăÊìÊłČúÆ·”ÄÏúÊÛÁżČ»”ÍÓÚ240șĐŁŹ”±ÏúÊÛ”„ŒÛÎȘ¶àÉÙÔȘʱŁŹĂżÌì»ńÈĄ”ÄÀûÈóŚîŽóŁŹŚîŽóÀûÈóÊǶàÉÙŁż
(3)žĂÍű”ê”êÖśÈÈĐÄč«ÒæÊÂÒ”ŁŹŸö¶šŽÓĂżÌì”ÄÏúÊÛÀûÈóÖĐŸèłö150ÔȘžűÏŁÍûč€łÌŁŹÎȘÁ˱ŁÖ€ŸèżîșóĂżÌìÊŁÓàÀûÈóČ»”ÍÓÚ3 600ÔȘŁŹÊÔÈ·¶šŐâÖÖÎäČęÓăÊìÊłČúÆ·ÏúÊÛ”„ŒÛ”Ä·¶Î§Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒ»ŽÎșŻÊę”ÄÍŒÏóŸčę”ă(©2ŁŹ12)șÍ(3ŁŹ©3)Łź
(1)ÇóŐâžöÒ»ŽÎșŻÊę”ıíŽïÊœŁź
(2)»łöŐâÌőÖ±Ïß”ÄÍŒÏóŁź
(3)ÉèŐâÌőÖ±ÏßÓëÁœŚű±êÖá”Äœ»”ă·Ö±đÎȘAĄąBŁŹÇóĄśAOB”ÄĂæ»ęŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
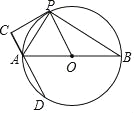
ĄŸÌâÄżĄżÈçÍŒŁŹÒŃÖȘABÊÇĄŃO”ÄÖ±Ÿ¶ŁŹPCÇĐĄŃOÓÚ”ăPŁŹčęAŚśÖ±ÏßACĄÍPCœ»ĄŃOÓÚÁíÒ»”ăDŁŹÁŹœÓPAĄąPBŁź
(1)ÇóÖ€ŁșAPÆœ·ÖĄÏCABŁ»
(2)ÈôPÊÇÖ±Ÿ¶ABÉÏ·œ°ëÔČ»ĄÉÏÒ»¶Ż”㣏ĄŃO”İ럶ÎȘ2ŁŹÔò
ąÙ”±ÏÒAP”Äł€ÊÇ_____ʱŁŹÒÔAŁŹOŁŹPŁŹCÎȘ¶„”ă”ÄËıßĐÎÊÇŐę·œĐÎŁ»
ąÚ”±![]() ”Äł€¶ÈÊÇ______ʱŁŹÒÔAŁŹDŁŹOŁŹPÎȘ¶„”ă”ÄËıßĐÎÊÇÁâĐÎŁź
”Äł€¶ÈÊÇ______ʱŁŹÒÔAŁŹDŁŹOŁŹPÎȘ¶„”ă”ÄËıßĐÎÊÇÁâĐÎŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
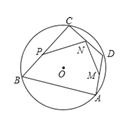
ĄŸÌâÄżĄżÈçÍŒŁŹABŁŹBCÊÇĄŃO”ÄÏÒŁŹĄÏBŁœ60ĄăŁŹ”ăOÔÚĄÏBÄÚŁŹ”ăDÎȘ![]() ÉϔĶŻ”㣏”ăMŁŹNŁŹP·Ö±đÊÇADŁŹDCŁŹCB”ÄÖД㣟ÈôĄŃO”İ럶ÎȘ2ŁŹÔòPN+MN”Äł€¶È”ÄŚîŽóÖ”ÊÇ________.
ÉϔĶŻ”㣏”ăMŁŹNŁŹP·Ö±đÊÇADŁŹDCŁŹCB”ÄÖД㣟ÈôĄŃO”İ럶ÎȘ2ŁŹÔòPN+MN”Äł€¶È”ÄŚîŽóÖ”ÊÇ________.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹ![]() ”ĶԜÇÏßÏàœ»ÓÚ”ă
”ĶԜÇÏßÏàœ»ÓÚ”ă![]() ŁŹÇÒ
ŁŹÇÒ![]() ŁŹčę”ă
ŁŹčę”ă![]() Śś
Śś![]() œ»
œ»![]() ÓÚ”ă
ÓÚ”ă![]() ŁŹÈô
ŁŹÈô![]() ”ÄÖÜł€ÎȘ20ŁŹÔò
”ÄÖÜł€ÎȘ20ŁŹÔò![]() ”ÄÖÜł€ÎȘŁš Ł©
”ÄÖÜł€ÎȘŁš Ł©
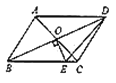
A. 7B. 8C. 9D. 10
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłÏŰŽÓÈ«ÏŰŸĆÄêŒ¶Ń§ÉúÖĐËæ»úłéÈĄÁËČż·ÖѧÉúœűĐĐÁËÒ»ŽÎÖĐżŒÌćÓężÆÄżČâÊÔ(°ŃČâÊÔœáčû·ÖÎȘËÄžö”ÈŒ¶Łș![]() Œ¶ŁșÓĆĐ㣻
Œ¶ŁșÓĆĐ㣻![]() Œ¶ŁșÁŒșĂŁ»
Œ¶ŁșÁŒșĂŁ»![]() Œ¶ŁșŒ°žńŁ»
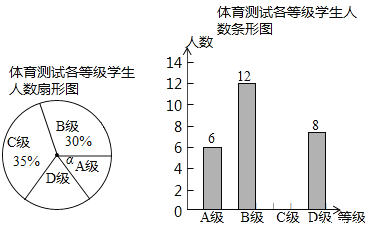
Œ¶ŁșŒ°žńŁ»![]() Œ¶ŁșČ»Œ°žń)ŁŹČąœ«ČâÊÔœáčû»æłÉÁËÈçÏÂÁœ·ùČ»ÍêŐû”ÄÍłŒÆÍŒ.ÇëžùŸĘÍłŒÆÍŒÖĐ”ÄĐĆÏąœâŽđÏÂÁĐÎÊÌâŁș
Œ¶ŁșČ»Œ°žń)ŁŹČąœ«ČâÊÔœáčû»æłÉÁËÈçÏÂÁœ·ùČ»ÍêŐû”ÄÍłŒÆÍŒ.ÇëžùŸĘÍłŒÆÍŒÖĐ”ÄĐĆÏąœâŽđÏÂÁĐÎÊÌâŁș
(1)±ŸŽÎłéŃùČâÊÔ”ÄѧÉúÈËÊęÊÇ ;
(2)ÈçÍŒÖĐ![]() ”ĶÈÊęÊÇ ŁŹČą°ŃÈçÍŒÌőĐÎÍłŒÆÍŒČčłäÍêŐûŁ»
”ĶÈÊęÊÇ ŁŹČą°ŃÈçÍŒÌőĐÎÍłŒÆÍŒČčłäÍêŐûŁ»
(3)ČâÊÔÀÏÊŠÏëŽÓ4λ͏ѧ(·Ö±đŒÇÎȘ![]() ŁŹÆäÖĐ
ŁŹÆäÖĐ![]() ÎȘĐĄĂś)ÖĐËæ»úŃĄÔńÁœÎ»ÍŹŃ§ÁËœâŃ”Á·ÇéżöŁŹÇëÓĂÁбí»ò»ÊśĐÎÍŒ”Ä·œ·šÇółöŃĄÖĐĐĄĂśžĆÂÊ.
ÎȘĐĄĂś)ÖĐËæ»úŃĄÔńÁœÎ»ÍŹŃ§ÁËœâŃ”Á·ÇéżöŁŹÇëÓĂÁбí»ò»ÊśĐÎÍŒ”Ä·œ·šÇółöŃĄÖĐĐĄĂśžĆÂÊ.
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com