
【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚.对于市场最为关注的产量和产量的稳定性,进行了抽样调查,过程如下,请补充完整.
收集数据 从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数:
甲 26 32 40 51 44 74 44 63 73 74 81 54 62 41 33 54 43 34 51 63 64 73 64 54 33
乙 27 35 46 55 48 36 47 68 82 48 57 66 75 27 36 57 57 66 58 61 71 38 47 46 71
整理、描述数据 按如下分组整理、描述这两组样本数据
个数 株数 大棚 |
|
|
|
|
|
|
甲 | 5 | 5 | 5 | 5 | 4 | 1 |
乙 | 2 | 4 | 6 | 2 |
(说明:45个以下为产量不合格,45个及以上为产量合格,其中45~65个为产量良好,65~85个为产量优秀)
分析数据 两组样本数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 众数 | 方差 |
甲 | 53 | 54 | 3047 |
乙 | 53 | 57 | 3022 |
得出结论:(1)估计乙大棚产量优秀的秧苗数为__________株;
(2)可以推断出__________大棚的小西红柿秧苗品种更适应市场需求,理由为_____________________.(至少从两个不同的角度说明推断的合理性)
【答案】(1)84;(2)乙;两组样本数据的平均数相同,但乙组数据的众数大,方差小,说明乙大棚的西红柿个头较大,且大小相对比较均匀.
【解析】
(1)根据收集数据填写表格即可求解;用乙组数据中产量优秀的株数除以25再乘以300即可得出答案;
(2)根据情况进行讨论分析,理由合理即可.
解:按如下分组整理、描述这两组样本数据:
个数 | 25≤x<35 | 35≤x<45 | 45≤x<55 | 55≤x<65 | 65≤x<75 | 75≤x<85 |
甲 | 5 | 5 | 5 | 5 | 4 | 1 |
乙 | 2 | 4 | 6 | 6 | 5 | 2 |
得出结论:
(1)估计乙大棚产量优秀的秧苗数为(5+2)÷25×300=84株;
故答案为:84
(2)乙大棚的小西红柿秧苗品种更适应市场需求,理由为两组样本数据的平均数相同,但乙组数据的众数大,方差小,说明乙大棚的西红柿个头较大,且大小相对比较均匀(答案不唯一,理由须支撑推断的合理性).
故答案为:乙;两组样本数据的平均数相同,但乙组数据的众数大,方差小,说明乙大棚的西红柿个头较大,且大小相对比较均匀.


科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
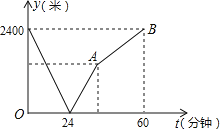
(1)根据图象信息,当t= 分钟时甲乙两人相遇,甲的速度为 米/分钟,乙的速度为 米/分钟;
(2)图中点A的坐标为 ;
(3)求线段AB所直线的函数表达式;
(4)在整个过程中,何时两人相距400米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点A在函数![]() (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA,交以A为圆心,AB为半径的圆弧于点D;延长BA,交以A为圆心,AC为半径的圆弧于点E.直线DE分别交x,y轴于点P,Q,当QE:DP=4:9时,图中阴影部分的面积等于____.
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA,交以A为圆心,AB为半径的圆弧于点D;延长BA,交以A为圆心,AC为半径的圆弧于点E.直线DE分别交x,y轴于点P,Q,当QE:DP=4:9时,图中阴影部分的面积等于____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,若点
中,若点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 和点
和点![]() 关于直线
关于直线![]() 对称,则称点
对称,则称点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点.
的二次对称点.
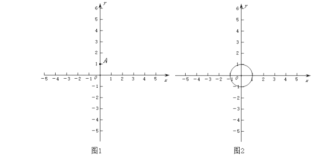
(1)如图1,点![]() .
.
①若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则点
的二次对称点,则点![]() 的坐标为________;
的坐标为________;
②若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则
的二次对称点,则![]() 的值为_______;
的值为_______;
③若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为__________;
的表达式为__________;
(2)如图2,![]() 的半径为1.若
的半径为1.若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直绩
轴,直绩![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在射线
在射线![]() 上,
上,![]() 的取值范围是________;
的取值范围是________;
(3)![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 的半径为2,若
的半径为2,若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在
在![]() 轴上,求
轴上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,若点
中,若点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 和点
和点![]() 关于直线
关于直线![]() 对称,则称点
对称,则称点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点.
的二次对称点.
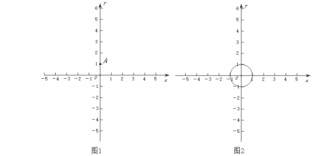
(1)如图1,点![]() .
.
①若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则点
的二次对称点,则点![]() 的坐标为________;
的坐标为________;
②若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则
的二次对称点,则![]() 的值为_______;
的值为_______;
③若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为__________;
的表达式为__________;
(2)如图2,![]() 的半径为1.若
的半径为1.若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直绩
轴,直绩![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在射线
在射线![]() 上,
上,![]() 的取值范围是________;
的取值范围是________;
(3)![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 的半径为2,若
的半径为2,若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在
在![]() 轴上,求
轴上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,以D为圆心,D长为半径作作⊙D.
⑴求证:AC是⊙D的切线.
⑵设AC与⊙D切于点E,DB=1,连接DE,BF,EF.
①当∠BAD= 时,四边形BDEF为菱形;
②当AB= 时,△CDE为等腰三角形.
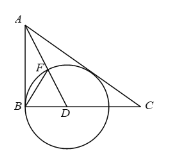
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )
A. ﹣![]() 或﹣12B. ﹣
或﹣12B. ﹣![]() 或2C. ﹣12或2D. ﹣
或2C. ﹣12或2D. ﹣![]() 或﹣12
或﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“新冠病毒”防控期间,某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售,两次购进同一商品的进价相同,具体情况如下表所示:
项目 | 购进数量(件) | 购进所需费用(元) | |
酒精消毒液 | 测温枪 | ||
第一次 | 30 | 40 | 8300 |
第二次 | 40 | 30 | 6400 |
(1)求酒精消毒液和测温枪两种商品每件的进价分别是多少元?
(2)公司决定酒精消毒液以每件20元出售,测温枪以每件240元出售.为满足市场需求,需购进这两种商品共1000件,且酒精消毒液的数量不少于测温枪数量的4倍,求该公司销售完上述1000件商品获得的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com