
ΓΨΧβΡΩΓΩ―ß–Θ”κΆΦ ιΙί‘ΎΆ§“ΜΧθ± ÷±Βά¬Ζ…œΘ§ΦΉ¥”―ß–Θ»ΞΆΦ ιΙίΘ§““¥”ΆΦ ιΙίΜΊ―ß–ΘΘ§ΦΉΓΔ““ΝΫ»ΥΕΦ‘»ΥΌ≤Ϋ––«“Ά§ ±≥ωΖΔΘ§““œ»ΒΫ¥οΡΩΒΡΒΊΘ°ΝΫ»Υ÷°ΦδΒΡΨύάκyΘ®ΟΉΘ©”κ ±ΦδtΘ®Ζ÷÷”Θ©÷°ΦδΒΡΚ· ΐΙΊœΒ»γΆΦΥυ ΨΘ°
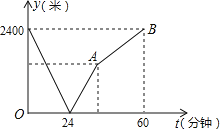
Θ®1Θ©ΗυΨίΆΦœσ–≈œΔΘ§Β±tΘΫΓΓ ΓΓΖ÷÷” ±ΦΉ““ΝΫ»Υœύ”ωΘ§ΦΉΒΡΥΌΕ»ΈΣΓΓ ΓΓΟΉ/Ζ÷÷”Θ§““ΒΡΥΌΕ»ΈΣΓΓ ΓΓΟΉ/Ζ÷÷”ΘΜ
Θ®2Θ©ΆΦ÷–ΒψAΒΡΉχ±ξΈΣΓΓ ΓΓΘΜ
Θ®3Θ©«σœΏΕΈABΥυ÷±œΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®4Θ©‘Ύ’ϊΗωΙΐ≥Χ÷–Θ§ΚΈ ±ΝΫ»ΥœύΨύ400ΟΉΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©24Θ§40Θ§60ΘΜΘ®2Θ©Θ®40Θ§1600Θ©ΘΜΘ®3Θ©œΏΕΈABΥυ±μ ΨΒΡΚ· ΐ±μ¥ο ΫΈΣyΘΫ40xΘΜΘ®4Θ©‘Ύ’ϊΗωΙΐ≥Χ÷–Θ§ΒΎ20Ζ÷÷”ΚΆ28Ζ÷÷” ±ΝΫ»ΥœύΨύ400ΟΉ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΆΦœσ–≈œΔΘ§Β±![]() Ζ÷÷” ±ΦΉ““ΝΫ»Υœύ”ωΘ§ΦΉ60Ζ÷÷”–– Μ2400ΟΉΘ§ΗυΨίΥΌΕ»
Ζ÷÷” ±ΦΉ““ΝΫ»Υœύ”ωΘ§ΦΉ60Ζ÷÷”–– Μ2400ΟΉΘ§ΗυΨίΥΌΕ»![]() ¬Ζ≥Χ
¬Ζ≥Χ![]() ±ΦδΩ…ΒΟΦΉΒΡΥΌΕ»Θ§ΫχΕχ«σ≥ω““ΒΡΥΌΕ»ΘΜ
±ΦδΩ…ΒΟΦΉΒΡΥΌΕ»Θ§ΫχΕχ«σ≥ω““ΒΡΥΌΕ»ΘΜ
Θ®2Θ©«σ≥ω““¥”ΆΦ ιΙίΜΊ―ß–ΘΒΡ ±ΦδΦ¥![]() ΒψΒΡΚαΉχ±ξΘΜ
ΒψΒΡΚαΉχ±ξΘΜ
Θ®3Θ©‘Υ”Ο¥ΐΕ®œΒ ΐΖ®«σΫβΦ¥Ω…ΘΜ
Θ®4Θ©Ζ÷œύ”ω«ΑΚσΝΫ÷÷«ιΩωΫβ¥πΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©ΗυΨίΆΦœσ–≈œΔΘ§Β±tΘΫ24Ζ÷÷” ±ΦΉ““ΝΫ»Υœύ”ωΘ§ΦΉΒΡΥΌΕ»ΈΣ2400Γ¬60ΘΫ40Θ®ΟΉ/Ζ÷÷”Θ©Θ°
ΓύΦΉΓΔ““ΝΫ»ΥΒΡΥΌΕ»ΚΆΈΣ2400Γ¬24ΘΫ100ΟΉ/Ζ÷÷”Θ§
Γύ““ΒΡΥΌΕ»ΈΣ100©¹40ΘΫ60Θ®ΟΉ/Ζ÷÷”Θ©Θ°
Ι ¥πΑΗΈΣΘΚ24Θ§40Θ§60ΘΜ
Θ®2Θ©““¥”ΆΦ ιΙίΜΊ―ß–ΘΒΡ ±ΦδΈΣ2400Γ¬60ΘΫ40Θ®Ζ÷÷”Θ©Θ§
40ΓΝ40ΘΫ1600Θ§
ΓύAΒψΒΡΉχ±ξΈΣΘ®40Θ§1600Θ©Θ°
Ι ¥πΑΗΈΣΘΚΘ®40Θ§1600Θ©ΘΜ
Θ®3Θ©…ηœΏΕΈABΥυ±μ ΨΒΡΚ· ΐ±μ¥ο ΫΈΣyΘΫkx+bΘ§
ΓΏAΘ®40Θ§1600Θ©Θ§BΘ®60Θ§2400Θ©Θ§
Γύ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§
ΓύœΏΕΈABΥυ±μ ΨΒΡΚ· ΐ±μ¥ο ΫΈΣyΘΫ40xΘΜ
Θ®4Θ©ΝΫ÷÷«ιΩωΘΚΔΌ”≠ΟφΘΚΘ®2400©¹400Θ©Γ¬100ΘΫ20Θ®Ζ÷÷”Θ©Θ§
ΔΎΉΏΙΐΘΚΘ®2400+400Θ©Γ¬100ΘΫ28Θ®Ζ÷÷”Θ©Θ§
Γύ‘Ύ’ϊΗωΙΐ≥Χ÷–Θ§ΒΎ20Ζ÷÷”ΚΆ28Ζ÷÷” ±ΝΫ»ΥœύΨύ400ΟΉΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
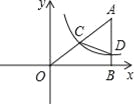
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–AΒψΒΡΉχ±ξΈΣΘ®8Θ§yΘ©Θ§ABΓΆx÷α”ΎΒψBΘ§sinΓœOAB=![]() Θ§Ζ¥±»άΐΚ· ΐy=
Θ§Ζ¥±»άΐΚ· ΐy=![]() ΒΡΆΦœσΒΡ“Μ÷ßΨ≠ΙΐAOΒΡ÷–ΒψCΘ§«“”κABΫΜ”ΎΒψDΘ°
ΒΡΆΦœσΒΡ“Μ÷ßΨ≠ΙΐAOΒΡ÷–ΒψCΘ§«“”κABΫΜ”ΎΒψDΘ°
Θ®1Θ©«σΖ¥±»άΐΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©»τΚ· ΐy=3x”κy=![]() ΒΡΆΦœσΒΡΝμ“Μ÷ßΫΜ”ΎΒψMΘ§«σ»ΐΫ«–ΈOMB”κΥΡ±Ώ–ΈOCDBΒΡΟφΜΐΒΡ±»Θ°
ΒΡΆΦœσΒΡΝμ“Μ÷ßΫΜ”ΎΒψMΘ§«σ»ΐΫ«–ΈOMB”κΥΡ±Ώ–ΈOCDBΒΡΟφΜΐΒΡ±»Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“ΜΗωΑκΨΕΈΣ![]() ΒΡ‘≤–Έ÷ΫΤ§‘Ύ±Ώ≥ΛΈΣ
ΒΡ‘≤–Έ÷ΫΤ§‘Ύ±Ώ≥ΛΈΣ![]() ΒΡΒ»±Ώ»ΐΫ«–ΈΡΎ»Έ“β‘ΥΕ·Θ§‘ρ‘ΎΗΟΒ»±Ώ»ΐΫ«–ΈΡΎΘ§’βΗω‘≤–Έ÷ΫΤ§ΓΑ≤ΜΡήΫ”¥ΞΒΫΒΡ≤ΩΖ÷Γ±ΒΡΟφΜΐ «____________.
ΒΡΒ»±Ώ»ΐΫ«–ΈΡΎ»Έ“β‘ΥΕ·Θ§‘ρ‘ΎΗΟΒ»±Ώ»ΐΫ«–ΈΡΎΘ§’βΗω‘≤–Έ÷ΫΤ§ΓΑ≤ΜΡήΫ”¥ΞΒΫΒΡ≤ΩΖ÷Γ±ΒΡΟφΜΐ «____________.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–Θ≥θΦΕ÷–―ß ΐ―ß–Υ»Λ–ΓΉιΈΣΝΥΫβ±Ψ–Θ―ß…ζΡξΝδ«ιΩωΘ§ΥφΜζΒς≤ιΝΥ±Ψ–Θ≤ΩΖ÷―ß…ζΒΡΡξΝδΘ§ΗυΨίΥυΒς≤ιΒΡ―ß…ζΒΡΡξΝδ(ΒΞΈΜΘΚΥξ)Θ§Μφ÷Τ≥ω»γœ¬ΒΡΆ≥ΦΤΆΦΔΌΚΆΆΦΔΎΘ§«κΗυΨίœύΙΊ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ

Θ®1Θ©±Ψ¥ΈΫ” ήΒς≤ιΒΡ―ß…ζ»Υ ΐΈΣ_______Θ§ΆΦΔΌ÷– ![]() ΒΡ÷ΒΈΣ ΘΜ
ΒΡ÷ΒΈΣ ΘΜ
Θ®2Θ©«σΆ≥ΦΤΒΡ’βΉι―ß…ζΡξΝδ ΐΨίΒΡΤΫΨυ ΐΓΔ÷Ύ ΐΚΆ÷–ΈΜ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–¬–ΆΙΎΉ¥≤ΓΕΨΖΈ―Ή“Ώ«ιΖΔ…ζΚσΘ§»Ϊ…γΜαΜΐΦΪ≤Έ”κ“Ώ«ιΖάΩΊΙΛΉςΘ§Ρ≥ –ΈΣΝΥΨΓΩλΆξ≥…100Άρ÷ΜΩΎ’÷ΒΡ…ζ≤ζ»ΈΈώΘ§Α≤≈≈ΦΉΓΔ““ΝΫΗω¥σ–ΆΙΛ≥ßΆξ≥…Θ°“―÷ΣΦΉ≥ßΟΩΧλΡή…ζ≤ζΩΎ’÷ΒΡ ΐΝΩ «““≥ßΟΩΧλΡή…ζ≤ζΩΎ’÷ΒΡ ΐΝΩΒΡ1.5±ΕΘ§≤Δ«“‘ΎΕάΝΔΆξ≥…60Άρ÷ΜΩΎ’÷ΒΡ…ζ≤ζ»ΈΈώ ±Θ§ΦΉ≥ß±»““≥ß…Ό”Ο5ΧλΘ°Έ ÷Ν…Ό”ΠΑ≤≈≈ΝΫΗωΙΛ≥ßΙΛΉςΕύ…ΌΧλ≤≈ΡήΆξ≥…»ΈΈώΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
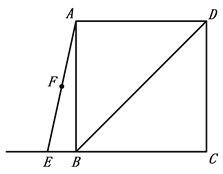
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ’ΐΖΫ–ΈABCD÷–Θ§Ν§Ϋ”BDΘ§ΒψEΈΣCB±ΏΒΡ―”≥ΛœΏ…œ“ΜΒψΘ§ΒψF «œΏΕΈAEΒΡ÷–ΒψΘ§ΙΐΒψFΉςAEΒΡ¥ΙœΏΫΜBD”ΎΒψM,Ν§Ϋ”MEΓΔMC.
Θ®1Θ©ΗυΨίΧβ“β≤Ι»ΪΆΦ–ΈΘ§≤¬œκ![]() ”κ
”κ![]() ΒΡ ΐΝΩΙΊœΒ≤Δ÷ΛΟςΘΜ
ΒΡ ΐΝΩΙΊœΒ≤Δ÷ΛΟςΘΜ
Θ®2Θ©Ν§Ϋ”FBΘ§≈–ΕœFB ΓΔFM÷°ΦδΒΡ ΐΝΩΙΊœΒ≤Δ÷ΛΟς.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΡΕΝ≤ΡΝœΘΚΉχ±ξΤΫΟφΡΎΘ§Ε‘”Ύ≈ΉΈοœΏyΘΫax2+bxΘ®aΓΌ0Θ©Θ§Έ“Ο«Α―ΒψΘ®©¹![]() Θ§
Θ§![]() Θ©≥ΤΈΣΗΟ≈ΉΈοœΏΒΡΫΙΒψΘ§Α―yΘΫ©¹
Θ©≥ΤΈΣΗΟ≈ΉΈοœΏΒΡΫΙΒψΘ§Α―yΘΫ©¹![]() ≥ΤΈΣΗΟ≈ΉΈοœΏΒΡΉΦœΏΖΫ≥ΧΘ°άΐ»γΘ§≈ΉΈοœΏyΘΫx2+2xΒΡΫΙΒψΈΣΘ®©¹1Θ§©¹
≥ΤΈΣΗΟ≈ΉΈοœΏΒΡΉΦœΏΖΫ≥ΧΘ°άΐ»γΘ§≈ΉΈοœΏyΘΫx2+2xΒΡΫΙΒψΈΣΘ®©¹1Θ§©¹![]() Θ©Θ§ΉΦœΏΖΫ≥Χ «yΘΫ©¹
Θ©Θ§ΉΦœΏΖΫ≥Χ «yΘΫ©¹![]() Θ°ΗυΨί≤ΡΝœΘ§œ÷“―÷Σ≈ΉΈοœΏyΘΫax2+bxΘ®aΓΌ0Θ©ΫΙΒψΒΡΉίΉχ±ξΈΣ3Θ§ΉΦœΏΖΫ≥ΧΈΣyΘΫ5Θ§‘ρΙΊ”ΎΕΰ¥ΈΚ· ΐyΘΫax2+bxΒΡΉν÷Β«ιΩωΘ§œ¬Ν–ΥΒΖ®÷–’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
Θ°ΗυΨί≤ΡΝœΘ§œ÷“―÷Σ≈ΉΈοœΏyΘΫax2+bxΘ®aΓΌ0Θ©ΫΙΒψΒΡΉίΉχ±ξΈΣ3Θ§ΉΦœΏΖΫ≥ΧΈΣyΘΫ5Θ§‘ρΙΊ”ΎΕΰ¥ΈΚ· ΐyΘΫax2+bxΒΡΉν÷Β«ιΩωΘ§œ¬Ν–ΥΒΖ®÷–’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
A.Ήν¥σ÷ΒΈΣ4B.Ήν–Γ÷ΒΈΣ4
C.Ήν¥σ÷ΒΈΣ3.5D.Ήν–Γ÷ΒΈΣ3.5
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
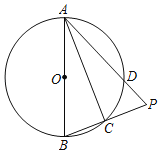
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡ±Ώ–ΈABCDΡΎΫ””ΎΓ―OΘ§AB «÷±ΨΕΘ§CΈΣ![]() ΒΡ÷–ΒψΘ§―”≥ΛADΘ§BCΫΜ”ΎPΘ§Ν§ΫαACΘ°
ΒΡ÷–ΒψΘ§―”≥ΛADΘ§BCΫΜ”ΎPΘ§Ν§ΫαACΘ°
Θ®1Θ©«σ÷ΛΘΚABΘΫAPΘΜ
Θ®2Θ©Β±ABΘΫ10Θ§DPΘΫ2 ±Θ§«σœΏΕΈCPΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΥ°ΙϊΜυΒΊΈΣΝΥ―Γ≥ω ”Π –≥Γ–η«σΒΡ–ΓΈςΚλ Ν―μΟγΘ§‘ΎΧθΦΰΜυ±ΨœύΆ§ΒΡ«ιΩωœ¬Θ§Α―ΝΫΗωΤΖ÷÷ΒΡ–ΓΈςΚλ Ν―μΟγΗς300÷ξΖ÷±π÷÷÷≤‘ΎΦΉΓΔ““ΝΫΗω¥σ≈οΘ°Ε‘”Ύ –≥ΓΉνΈΣΙΊΉΔΒΡ≤ζΝΩΚΆ≤ζΝΩΒΡΈ»Ε®–‘Θ§Ϋχ––ΝΥ≥ι―υΒς≤ιΘ§Ιΐ≥Χ»γœ¬Θ§«κ≤Ι≥δΆξ’ϊΘ°
’Φ· ΐΨί ¥”ΦΉΓΔ““ΝΫΗω¥σ≈οΗς ’Φ·ΝΥ25÷ξ―μΟγ…œΒΡ–ΓΈςΚλ ΝΒΡΗω ΐΘΚ
ΦΉ 26 32 40 51 44 74 44 63 73 74 81 54 62 41 33 54 43 34 51 63 64 73 64 54 33
““ 27 35 46 55 48 36 47 68 82 48 57 66 75 27 36 57 57 66 58 61 71 38 47 46 71
’ϊάμΓΔΟη ω ΐΨί Α¥»γœ¬Ζ÷Ήι’ϊάμΓΔΟη ω’βΝΫΉι―υ±Ψ ΐΨί
Ηω ΐ ÷ξ ΐ ¥σ≈ο |
|
|
|
|
|
|
ΦΉ | 5 | 5 | 5 | 5 | 4 | 1 |
““ | 2 | 4 | 6 | 2 |
Θ®ΥΒΟςΘΚ45Ηω“‘œ¬ΈΣ≤ζΝΩ≤ΜΚœΗώΘ§45ΗωΦΑ“‘…œΈΣ≤ζΝΩΚœΗώΘ§Τδ÷–45ΓΪ65ΗωΈΣ≤ζΝΩΝΦΚΟΘ§65ΓΪ85ΗωΈΣ≤ζΝΩ”≈–ψΘ©
Ζ÷Έω ΐΨί ΝΫΉι―υ±Ψ ΐΨίΒΡΤΫΨυ ΐΓΔ÷Ύ ΐΚΆΖΫ≤ν»γœ¬±μΥυ ΨΘΚ
¥σ≈ο | ΤΫΨυ ΐ | ÷Ύ ΐ | ΖΫ≤ν |
ΦΉ | 53 | 54 | 3047 |
““ | 53 | 57 | 3022 |
ΒΟ≥ωΫα¬έΘΚΘ®1Θ©ΙάΦΤ““¥σ≈ο≤ζΝΩ”≈–ψΒΡ―μΟγ ΐΈΣ__________÷ξΘΜ
Θ®2Θ©Ω…“‘ΆΤΕœ≥ω__________¥σ≈οΒΡ–ΓΈςΚλ Ν―μΟγΤΖ÷÷Ηϋ ”Π –≥Γ–η«σΘ§άμ”…ΈΣ_____________________Θ°Θ®÷Ν…Ό¥”ΝΫΗω≤ΜΆ§ΒΡΫ«Ε»ΥΒΟςΆΤΕœΒΡΚœάμ–‘Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com