
【题目】阅读材料:坐标平面内,对于抛物线y=ax2+bx(a≠0),我们把点(﹣![]() ,
,![]() )称为该抛物线的焦点,把y=﹣
)称为该抛物线的焦点,把y=﹣![]() 称为该抛物线的准线方程.例如,抛物线y=x2+2x的焦点为(﹣1,﹣
称为该抛物线的准线方程.例如,抛物线y=x2+2x的焦点为(﹣1,﹣![]() ),准线方程是y=﹣
),准线方程是y=﹣![]() .根据材料,现已知抛物线y=ax2+bx(a≠0)焦点的纵坐标为3,准线方程为y=5,则关于二次函数y=ax2+bx的最值情况,下列说法中正确的是( )
.根据材料,现已知抛物线y=ax2+bx(a≠0)焦点的纵坐标为3,准线方程为y=5,则关于二次函数y=ax2+bx的最值情况,下列说法中正确的是( )
A.最大值为4B.最小值为4
C.最大值为3.5D.最小值为3.5
科目:初中数学 来源: 题型:
【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
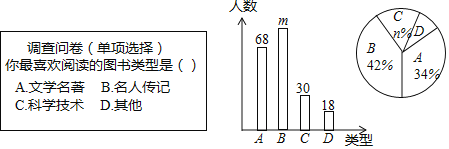
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
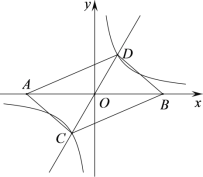
【题目】如图,在平面直角坐标系中,点A的坐标为(m,0),m<0,点B与点A 关于原点对称,直线![]() 与双曲线
与双曲线![]() 交于C,D两点.
交于C,D两点.
(1)直接判断后填空:四边形ACBD的形状一定是 ;
(2)若点D(1,t),求双曲线的解析式;
(3)在(2)的前提下,四边形ACBD为矩形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
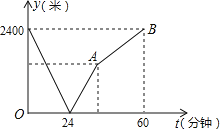
(1)根据图象信息,当t= 分钟时甲乙两人相遇,甲的速度为 米/分钟,乙的速度为 米/分钟;
(2)图中点A的坐标为 ;
(3)求线段AB所直线的函数表达式;
(4)在整个过程中,何时两人相距400米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家快递公司揽件员(揽收快件的员工)的日工资方案如下:
甲公司为“基本工资+揽件提成”,其中基本工资为70元/日,每揽收一件提成2元;
乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过40,每件提成4元;若当日搅件数超过40,超过部分每件多提成2元.
如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图:
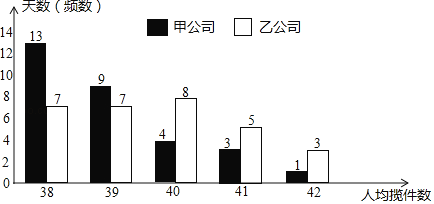
(1)现从今年四月份的30天中随机抽取1天,求这一天甲公司揽件员人均揽件数超过40(不含40)的概率;
(2)根据以上信息,以今年四月份的数据为依据,并将各公司揽件员的人均揽件数视为该公司各揽件员的
揽件数,解决以下问题:
①估计甲公司各揽件员的日平均件数;
②小明拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,井说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是AB上一点,以点D为圆心,AC为半径画弧交BA的延长线于点E,连接CD,作EF∥CD,交∠EAC的平分线于点F,连接CF.
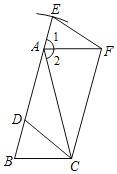
(1)求证:△BCD≌△AFE;
(2)若AC=6,∠BAC=30°,求四边形CDEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,![]() ,
,![]() 的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )

A.17B.18C.19D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点A在函数![]() (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA,交以A为圆心,AB为半径的圆弧于点D;延长BA,交以A为圆心,AC为半径的圆弧于点E.直线DE分别交x,y轴于点P,Q,当QE:DP=4:9时,图中阴影部分的面积等于____.
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA,交以A为圆心,AB为半径的圆弧于点D;延长BA,交以A为圆心,AC为半径的圆弧于点E.直线DE分别交x,y轴于点P,Q,当QE:DP=4:9时,图中阴影部分的面积等于____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,以D为圆心,D长为半径作作⊙D.
⑴求证:AC是⊙D的切线.
⑵设AC与⊙D切于点E,DB=1,连接DE,BF,EF.
①当∠BAD= 时,四边形BDEF为菱形;
②当AB= 时,△CDE为等腰三角形.
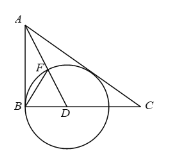
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com