
【题目】如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,以D为圆心,D长为半径作作⊙D.
⑴求证:AC是⊙D的切线.
⑵设AC与⊙D切于点E,DB=1,连接DE,BF,EF.
①当∠BAD= 时,四边形BDEF为菱形;
②当AB= 时,△CDE为等腰三角形.
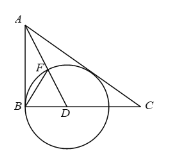
【答案】(1)见解析;(2)①30°,②![]() +1
+1
【解析】
(1) 作DE⊥AC于M,由∠ABC=90°,进一步说明DM=DB,即DB是⊙D的半径,即可完成证明;
(2)①先说明△BDF是等边三角形,再运用直角三角形的内角和定理解答即可;②先说明DE=CE=BD=1,再设AB=x,则AE=x,分别表示出AC、BC、AB的长,然后再运用 勾股定理 解答即可.
⑴证明:如图:作DE⊥AC于M,
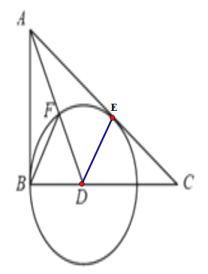
∵∠ABC=90°,∠BAC的平分线交BC于点D,
∴DE=DB.
∴DM是⊙D的半径,
∴AC是⊙D的切线;
⑵①如图:
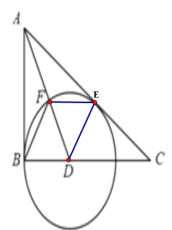
∵四边形BDEF为菱形;
∴△BDF是等边三角形
∴∠ADB=60°
∴∠BAD=90°-60°=30°
∴当∠BAD=30°时,四边形BDEF为菱形;
②∵△CDE为等腰三角形.
∴DE=CE=BD=1,
∴DC=![]()
设AB=x,则AE=x
∴在Rt△ABC中,AB=x,AC=1+x,BC=1+![]()
∴![]() ,解得x=
,解得x=![]() +1
+1
∴当AB=![]() +1时,△CDE为等腰三角形.
+1时,△CDE为等腰三角形.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:坐标平面内,对于抛物线y=ax2+bx(a≠0),我们把点(﹣![]() ,
,![]() )称为该抛物线的焦点,把y=﹣
)称为该抛物线的焦点,把y=﹣![]() 称为该抛物线的准线方程.例如,抛物线y=x2+2x的焦点为(﹣1,﹣
称为该抛物线的准线方程.例如,抛物线y=x2+2x的焦点为(﹣1,﹣![]() ),准线方程是y=﹣
),准线方程是y=﹣![]() .根据材料,现已知抛物线y=ax2+bx(a≠0)焦点的纵坐标为3,准线方程为y=5,则关于二次函数y=ax2+bx的最值情况,下列说法中正确的是( )
.根据材料,现已知抛物线y=ax2+bx(a≠0)焦点的纵坐标为3,准线方程为y=5,则关于二次函数y=ax2+bx的最值情况,下列说法中正确的是( )
A.最大值为4B.最小值为4
C.最大值为3.5D.最小值为3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D.过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
(1)求证:BC是⊙O的切线;
(2)若AC=6,BC=8,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚.对于市场最为关注的产量和产量的稳定性,进行了抽样调查,过程如下,请补充完整.
收集数据 从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数:
甲 26 32 40 51 44 74 44 63 73 74 81 54 62 41 33 54 43 34 51 63 64 73 64 54 33
乙 27 35 46 55 48 36 47 68 82 48 57 66 75 27 36 57 57 66 58 61 71 38 47 46 71
整理、描述数据 按如下分组整理、描述这两组样本数据
个数 株数 大棚 |
|
|
|
|
|
|
甲 | 5 | 5 | 5 | 5 | 4 | 1 |
乙 | 2 | 4 | 6 | 2 |
(说明:45个以下为产量不合格,45个及以上为产量合格,其中45~65个为产量良好,65~85个为产量优秀)
分析数据 两组样本数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 众数 | 方差 |
甲 | 53 | 54 | 3047 |
乙 | 53 | 57 | 3022 |
得出结论:(1)估计乙大棚产量优秀的秧苗数为__________株;
(2)可以推断出__________大棚的小西红柿秧苗品种更适应市场需求,理由为_____________________.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个三角形绕其中一个顶点逆时针旋转并放大或缩小(这个顶点不变),我们把这样的三角形
运动称为三角形的T-变换,这个顶点称为T-变换中心,旋转角称为T-变换角,三角形与原三角形的对应边
之比称为T-变换比;已知△![]() 在直角坐标平面内,点
在直角坐标平面内,点![]() ,
,![]() ,
,![]() ,将△
,将△![]() 进
进
行T-变换,T-变换中心为点![]() ,T-变换角为60°,T-变换比为
,T-变换角为60°,T-变换比为![]() ,那么经过T-变换后点
,那么经过T-变换后点![]() 所对应的点的
所对应的点的
坐标为 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
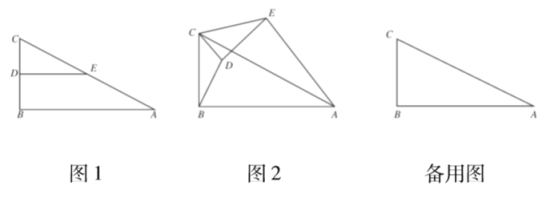
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,连接
的中点,连接![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转,记旋转角为
按顺时针方向旋转,记旋转角为![]() .
.
(1)问题发现
①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() .
.
(2)拓展探究
试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当![]() 旋转至A、B、E三点共线时,直接写出线段
旋转至A、B、E三点共线时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
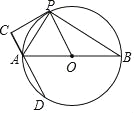
【题目】如图,已知AB是⊙O的直径,PC切⊙O于点P,过A作直线AC⊥PC交⊙O于另一点D,连接PA、PB.
(1)求证:AP平分∠CAB;
(2)若P是直径AB上方半圆弧上一动点,⊙O的半径为2,则
①当弦AP的长是_____时,以A,O,P,C为顶点的四边形是正方形;
②当![]() 的长度是______时,以A,D,O,P为顶点的四边形是菱形.
的长度是______时,以A,D,O,P为顶点的四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)B(-1,-2)两点,与![]() 轴相交于点C.
轴相交于点C.
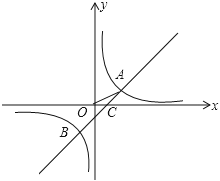
(1)分别求反比例函数和一次函数的解析式(关系式);
(2)连接OA,求△AOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com