
【题目】如图,![]() 的边
的边![]() 与经过
与经过![]() 三点的
三点的![]() 相切.
相切.
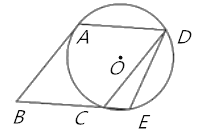
(1)求证:弧![]() 弧
弧![]() ;
;
(2)如图2,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 若
若![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接AO并延长交DC于F.只要证明AF⊥DC,利用垂径定理即可解决问题;
(2)作出如图的辅助线,证得四边形ACED是等腰梯形结合(1)的结论得到AC=AD=DE,CM=EN,AM=DN,CE=MN,根据![]() ,设DE=
,设DE=![]() ,则EN=
,则EN=![]() ,DN
,DN![]() ,通过计算即可求解.
,通过计算即可求解.
(1)连接AO并延长交BC于F.
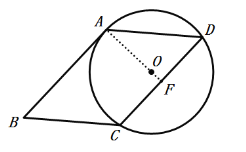
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠FAB=∠DFA,
∵AB是⊙O的切线,
∴∠FAB =90°,
∴∠DFA =90°,
∴OF⊥DC,
∴A是![]() 的中点,
的中点,
∴![]() =
=![]() ;
;
(2)如图,作CM⊥AD于M,EN⊥AD于N,连接AC.

由(1)得:A是![]() 的中点,
的中点,
∴AC=AD,
∵四边形ABCD是平行四边形,
∴![]() =
=![]() ,CE∥AD,
,CE∥AD,
∴AC=AD=DE,∠ADC=∠DCE,
∴四边形ACED是等腰梯形,
∴CM=EN,AM=DN,CE=MN,
∵![]() ,
,
设DE=![]() ,则EN=
,则EN=![]() ,DN=
,DN=![]() ,
,
∴CM=EN=![]() ,DM=AD-AM=DE-DN=
,DM=AD-AM=DE-DN=![]() ,
,
∴![]() .
.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,若点
中,若点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 和点
和点![]() 关于直线
关于直线![]() 对称,则称点
对称,则称点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点.
的二次对称点.
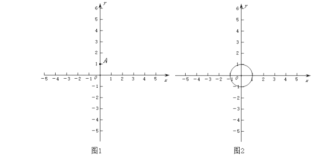
(1)如图1,点![]() .
.
①若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则点
的二次对称点,则点![]() 的坐标为________;
的坐标为________;
②若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则
的二次对称点,则![]() 的值为_______;
的值为_______;
③若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为__________;
的表达式为__________;
(2)如图2,![]() 的半径为1.若
的半径为1.若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直绩
轴,直绩![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在射线
在射线![]() 上,
上,![]() 的取值范围是________;
的取值范围是________;
(3)![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 的半径为2,若
的半径为2,若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在
在![]() 轴上,求
轴上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数(k>0,x>0)的图象经过AC的中点D,则k的值为( )
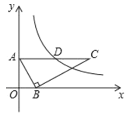
A.8B.5C.6D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把八个完全相同的小球平分为两组,每组中每个分别写上1,2,3,4四个数字,然后分别装入不透明的口袋内搅匀,从第一个口袋内取出一个数记下数字后作为点P的横坐标x,然后再从第二个口袋中取出一个球记下数字后作为点P的纵坐标,则点P(x,y)落在直线y=﹣x+5上的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“新冠病毒”防控期间,某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售,两次购进同一商品的进价相同,具体情况如下表所示:
项目 | 购进数量(件) | 购进所需费用(元) | |
酒精消毒液 | 测温枪 | ||
第一次 | 30 | 40 | 8300 |
第二次 | 40 | 30 | 6400 |
(1)求酒精消毒液和测温枪两种商品每件的进价分别是多少元?
(2)公司决定酒精消毒液以每件20元出售,测温枪以每件240元出售.为满足市场需求,需购进这两种商品共1000件,且酒精消毒液的数量不少于测温枪数量的4倍,求该公司销售完上述1000件商品获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
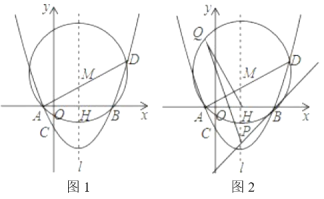
【题目】如图1,在平面直角坐标系中,抛物线y![]() x2bxc交x轴于点A,B,点B的坐标为(4,0),与y轴于交于点C(0,﹣2).
x2bxc交x轴于点A,B,点B的坐标为(4,0),与y轴于交于点C(0,﹣2).
(1)求此抛物线的解析式;
(2)在抛物线上取点D,若点D的横坐标为5,求点D的坐标及∠ADB的度数;
(3)在(2)的条件下,设抛物线对称轴![]() 交x轴于点H,△ABD的外接圆圆心为M(如图1),
交x轴于点H,△ABD的外接圆圆心为M(如图1),
①求点M的坐标及⊙M的半径;
②过点B作⊙M的切线交![]() 于点P(如图2),设Q为⊙M上一动点,则在点Q运动过程中
于点P(如图2),设Q为⊙M上一动点,则在点Q运动过程中![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
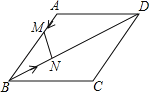
【题目】如图所示,菱形ABCD的边长是2厘米,∠BAD=120°,动点M以1厘米/秒的速度自A点出发向B移动,动点N以2厘米/移的速度自B点出发向D移动,两点中任一个到达线段端点移动便告结束.若点M、N同时出发运动了t秒,记△BMN的面积为S厘米2,下面图象中能表示S与t之间的函数关系的是( )
A.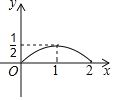 B.
B.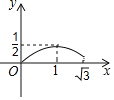
C.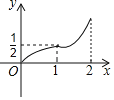 D.
D.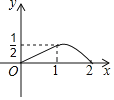
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com