
分析 镜框所占的面积为照片面积的四分之一,为了不出差错,最好表示出总面积-照片的面积=镜框的面积.那么镜框的面积=$\frac{1}{4}$照片的面积.
解答 解:设镜框边的宽度应是x厘米,
根据题意得:(28+2x)(20+2x)-28×20=$\frac{1}{4}$×28×20,
x2+24x-35=0,
(x+12)2=179,
x1=-12-$\sqrt{179}$(舍),x2=-12+$\sqrt{179}$≈-12+13.4≈1.4,
答:镜框边的宽度应是1.4厘米.
点评 本题考查了由实际问题抽象出一元二次方程的知识,本题要通过设未知数来表示整个图形的长、宽,再分析整个图形面积与相片面积的关系列方程.注意边框是正数,把负的舍去.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
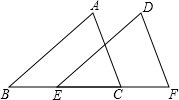 如图,已知点B、E、C、F在同一直线上,且BE=CF,∠ABC=∠DEF,那么添加一个条件后.仍无法判定△ABC≌△DEF的是( )
如图,已知点B、E、C、F在同一直线上,且BE=CF,∠ABC=∠DEF,那么添加一个条件后.仍无法判定△ABC≌△DEF的是( )| A. | AC=DF | B. | AB=DE | C. | AC∥DF | D. | ∠A=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向上、直线x=4、(4,5) | B. | 向上、直线x=-4、(-4,5) | ||
| C. | 向下、直线x=4、(4,5) | D. | 向下、直线x=-4、(-4,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com