Question

14．已知∠BAK=90°，在∠BAK的边AK上有一点C
（1）分别以AB，BC为边在角的内部作等边△ABD和等边△BCE，连接ED交AC于P，求证：PA=PD；
（2）在（1）的条件下．将△ABD和△BCE同时绕点B逆时针旋转β角，得到△BA′D′．和△BC′E′，连接A′E′，C′D′，M，N分别为A′E′，C′D′的中点，试判断MN与D′E′的数量关系，并证明；
（3）E为角内一点，连接CE，在CE右侧作△CEM，且∠EMC=90°，EM=CM，连接BE，N为BE的中点，连接AM，AN，若AC=AB=$\sqrt{3}$，∠ECK=75°，EC=$\sqrt{6}$，求AN的长．

Answer 1

分析 （1）只要证明△BAC≌△BDE，推出∠BAC=∠BDE=90°，推出∠PDA=180°-60°-90°=30°，∠PAD=90°-60°=30°，推出∠PAD=∠PDA=30°即可证明．
（2）结论：D′E′=2MN．如图2中，连接D′E′，取C′E′的中点F，A′D′的中点G，连接NF、FM、GM、NG．先证明四边形NGMF是平行四边形，再证明△FNM是等边三角形，即可解决问题．
（3）如图3中，连接AM、BC、CN、MN，作MH⊥AK于H．想办法证明△AMN是等腰直角三角形，利用勾股定理求出AM即可解决问题．

解答 （1）证明：如图1中，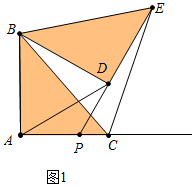

∵△ABD，△BCE都是等边三角形，
∴BA=BD，BC=BE，∠ABD=∠CBE=∠BAD=∠BDA=60°，
∴∠BAC=∠DBE，
在△BAC和△BDE中，
$\left\{\begin{array}{l}{BA=BD}\\{∠BAC=∠DBE}\\{BC=BE}\end{array}\right.$，
∴△BAC≌△BDE，
∴∠BAC=∠BDE=90°，
∴∠PDA=180°-60°-90°=30°，∠PAD=90°-60°=30°，
∴∠PAD=∠PDA=30°，
∴PA=PD．

（2）解：结论：D′E′=2MN．理由如下，
如图2中，连接D′E′，取C′E′的中点F，A′D′的中点G，连接NF、FM、GM、NG．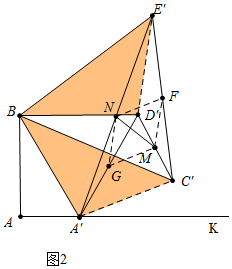

由（1）可知△BA′C′≌△D′BE，
∴A′C′=D′E′，∠A′C′B=∠BED′，
∵E′N=NA′，E′F=DC′，
∴FN∥A′C′，FN=$\frac{1}{2}$A′C′，同理可证GM∥A′C′，GM=$\frac{1}{2}$A′C′，FM=$\frac{1}{2}$D′E′，
∴NF=GM．NF∥MG，
∴四边形NGMF是平行四边形，FN=FM，
∵∠MFN=180°-（∠E′FN+∠MFC′）=180°-（∠A′C′E′+∠C′E′D′）=180°-（60°+∠A′C′B+∠C′E′D′）=180°-（60°+∠BE′D′+∠C′E′D′）=60°，
∴△FNM是等边三角形，
∴MN=FM，
∴E′D′=2MN．

（3）解：如图3中，连接AM、BC、CN、MN，作MH⊥AK于H．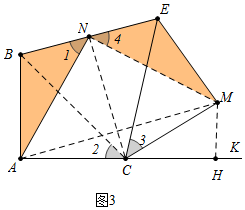

∵AB=AC=$\sqrt{3}$，∠BAC=90°，
∴BC=$\sqrt{A{B}^{2}+C{B}^{2}}$=$\sqrt{6}$，
∵EC=$\sqrt{6}$，CM=EM，∠CME=90°，
∴CM=ME=$\sqrt{3}$，BC=EC，
∴AB=EN，
∵BN=NE，
∴CN⊥BE，
∴∠CNB=∠CNE=90°，
∵∠BAC+∠CNB=180°，
∴A、C、N、B四点共圆，
∴∠1=∠2=45°，同理∠3=∠4=45°，
∴∠ANM=90°，
∵∠ECH=75°，∠ACB=45°，
∴∠BCE=60°，
∴△BCE是等边三角形，
∴∠CBE=∠CEB=60°，
∴∠ABN=∠NEM=105°，
在△ABN和△MEN中，
$\left\{\begin{array}{l}{AB=EM}\\{∠ABN=∠MEN}\\{BN=NE}\end{array}\right.$，
∴△ABN≌△MEN，
∴AN=MN，
∴△AMN是等腰直角三角形，
在Rt△CMH中，∵∠MHC=90°，CM=$\sqrt{3}$，
∴MH=$\frac{\sqrt{3}}{2}$，CH=$\frac{3}{2}$，AH=$\sqrt{3}$+$\frac{3}{2}$，
∴AM=$\sqrt{A{H}^{2}+M{H}^{2}}$=$\sqrt{（\sqrt{3}+\frac{3}{2}）^{2}+（\frac{\sqrt{3}}{2}）^{2}}$=$\frac{3\sqrt{2}+\sqrt{6}}{2}$，
∴AN=$\frac{\sqrt{2}}{2}$AM=$\frac{3+\sqrt{3}}{2}$．

点评 本题考查几何变换综合题、等腰直角三角形的判定和性质、全等三角形的判定和性质、勾股定理、四点共圆等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造全等三角形，属于中考压轴题．