
【题目】下列关于函数![]() 的四个命题:
的四个命题:
①当x=0时,y有最小值6;
② m为任意实数,x=2-m时的函数值大于x=2+m时的函数值;
③若函数图象过点(a,m0) 和(b, m0+1),其中a>0,b>2,则a<b;
④若m>2,且m是整数,当m≤x≤m+1 时,y的整数值有(2m-2)个.
其中真命题有______个.
【答案】2
【解析】
分别根据二次函数的图像与系数的关系、抛物线的顶点坐标公式以及增减性解题,见详解.
解:①当x=0时,y=6,此时6不是抛物线的最小值,错误,
② 当m=0时,x=2-m等于x=2+m时的函数值,错误,
③若函数图象过点(a,m0) 和(b, m0+1),m0+1![]() m0,函数的对称轴为直线x=2,
m0,函数的对称轴为直线x=2,
∴当x![]() 2时,y随x的增大而增大,
2时,y随x的增大而增大,
∴当![]() 时, a<b;当
时, a<b;当![]() 时, a<b成立,∴③正确,
时, a<b成立,∴③正确,
④当x=m+1时,
y=(m+1)2-4(m+1)+6,
当x=m时,
y=m2-4m+6,
(m+1)2-4(m+1)+6- m2-4m+6=2m-3,
∵m是整数,
∴2m-3是整数,
∴y的整数值有(2m-2)个,故④正确.


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a>0)经过点A(-3![]() ,0)、B(
,0)、B(![]() ,0),它与y轴相交于点C,且∠ACB≥90°,设该抛物线的顶点为D,△BCD的边CD上的高为h.
,0),它与y轴相交于点C,且∠ACB≥90°,设该抛物线的顶点为D,△BCD的边CD上的高为h.
(1)求实数a的取值范围;
(2)求高h的取值范围;
(3)当(1)的实数a取得最大值时,求此时△BCD外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
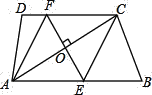
【题目】如图,在四边形ABCD中,![]() ,过对角线AC的中点O作
,过对角线AC的中点O作![]() ,分别交边AB,CD于点E,F,连接CE,AF.
,分别交边AB,CD于点E,F,连接CE,AF.
![]() 求证:四边形AECF是菱形;
求证:四边形AECF是菱形;
![]() 若
若![]() ,OF:
,OF:![]() :5,求四边形AECF的面积.
:5,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
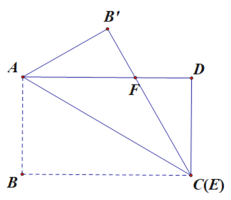
【题目】如图,在矩形纸片ABCD中,已知AB=2,BC=![]() ,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.
,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.
(1)当点E与点C重合时,求DF的长;
(2)若B′C′分别交边AD,CD于点F,G,且∠DAE=22.5°,求△DFG的面积;
(3)如果点M为CD的中点,那么在点E从点C移动到点D的过程中,求C′M的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
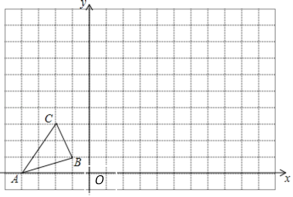
【题目】如图,在 11×16 的网格图中,△ABC 三个顶点坐标分别为 A(﹣4,0),B(﹣1,1),C(﹣2,3).
(1)请画出△ABC 沿x 轴正方向平移4个单位长度所得到的△A1B1C1;
(2)以原点O为位似中心,将(1)中的△A1B1C1 放大为原来的3倍得到△A2B2C2,请在第一象限内画出△A2B2C2,并直接写出△A2B2C2 三个顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
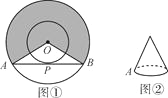
【题目】如图①,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1.
(1)用阴影部分的扇形围成一个圆锥(OA与OB重合),求该圆锥的底面半径.
(2)用余下部分再围成一个圆锥(如图②所示),若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到A点,求小虫爬行的最短路线的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com