
【题目】抛物线y=ax2+bx+c(a>0)经过点A(-3![]() ,0)、B(
,0)、B(![]() ,0),它与y轴相交于点C,且∠ACB≥90°,设该抛物线的顶点为D,△BCD的边CD上的高为h.
,0),它与y轴相交于点C,且∠ACB≥90°,设该抛物线的顶点为D,△BCD的边CD上的高为h.
(1)求实数a的取值范围;
(2)求高h的取值范围;
(3)当(1)的实数a取得最大值时,求此时△BCD外接圆的半径.
【答案】(1)0<a≤![]() ;(2)0<h≤
;(2)0<h≤![]() ;(3)2
;(3)2![]() .
.
【解析】
(1)利用直角三角形各边的关系,求得OC2=OAOB,利用边角关系,代入a值解得.
(2)过D作DE⊥OC,延长DC交x轴于点H,过点B作BF⊥CH于点F.利用顶点公式求得点D,由OC≤3,则tan∠OHC=![]() ≤
≤![]() ,从而解得.
,从而解得.
(3)求得a的最大值,求得h值,可得BD,BC,连接DG,由△DGB∽△BCF求得DG.
解:(1)当∠ACB=90°时,OC2=OAOB,
得OC=3
又∠ACB≥90°,
故OC≤3,
所以9a≤3,
∴0<a≤![]() .
.
(2)过D作DE⊥OC,延长DC交x轴于点H,过点B作BF⊥CH于点F.
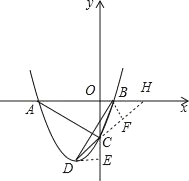
因为D为抛物线的顶点,
所以D(-![]() ,﹣12a),OE=12a,
,﹣12a),OE=12a,
又∵OC=9a,CE=3a,DE=![]() ,
,
易证△HCO∽△DCE,
有![]() =3,
=3,
故OH=3DE=3![]() ,BH=OH﹣OB=2
,BH=OH﹣OB=2![]() ,
,
又OC≤3,则tan∠OHC=![]() ≤
≤![]() ,
,
于是0<∠OHC<30°,
则h=BF=BHsin∠BHF≤BHsin30°=![]() ,
,
从而0<h≤![]() .
.
(3)当a取最大值时,a=![]() ,
,
此时h=![]() ,B(
,B(![]() ,0),C(0,﹣3),D(-
,0),C(0,﹣3),D(-![]() ,﹣4),
,﹣4),
可求BD=2![]() ,BC=2
,BC=2![]() ,
,
作直径DG,易证△DGB∽△BCF,![]() ,
,

所以![]() .
.
故DG=4![]() ,
,
即△BCD外接圆的半径为2![]() .
.


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
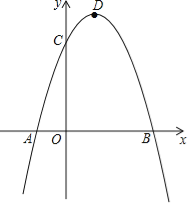
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
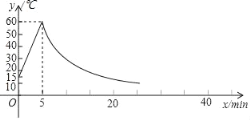
【题目】制作一种产品,需先将材料加热达到60℃后,再进行操作,设该材料温度为y(℃)从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系:停止加热进行操作时,温度y与时间x成反比例关系(如图).已知在操作加热前的温度为15℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式为“单人组”和“双人组”.小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个梯子AB斜靠在一竖直的墙AO上,测得AO=2 m.若梯子的顶端沿墙下滑0.5米,这时梯子的底端也恰好外移0.5米,则梯子的长度AB为( )
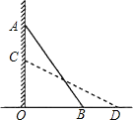
A. 2.5 m B. 3 m C. 1.5 m D. 3.5 m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域为响应“绿水青山就是金山银山”的号召,加强了绿化建设.为了解该区域群众对绿化建设的满意程度,某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查,得到如下不完整统计图.
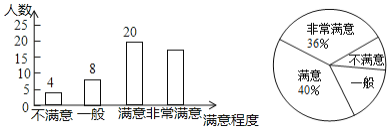
请结合图中信息,解决下列问题:
(1)此次调查中接受调查的人数为多少人,其中“非常满意”的人数为多少人;
(2)兴趣小组准备从“不满意”的4位群众中随机选择2位进行回访,已知这4位群众中有2位来自甲片区,另2位来自乙片区,请用画树状图或列表的方法求出选择的群众来自甲片区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (x>0)交于点A,将直线y=
(x>0)交于点A,将直线y=![]() x向右平移3个单位后,与双曲线y=
x向右平移3个单位后,与双曲线y=![]() (x>0)交于点B,与x轴交于点C,若
(x>0)交于点B,与x轴交于点C,若![]() =2,则k=( )
=2,则k=( )

A. ![]() B. 4 C. 6 D.
B. 4 C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数![]() 的四个命题:
的四个命题:
①当x=0时,y有最小值6;
② m为任意实数,x=2-m时的函数值大于x=2+m时的函数值;
③若函数图象过点(a,m0) 和(b, m0+1),其中a>0,b>2,则a<b;
④若m>2,且m是整数,当m≤x≤m+1 时,y的整数值有(2m-2)个.
其中真命题有______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
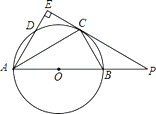
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC、BC.
(1)求证:AC平分∠BAD.
(2)求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com