
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
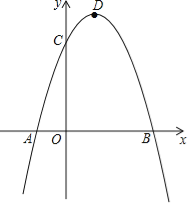
(1)求此二次函数解析式;
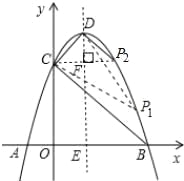
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式为y=﹣x2+2x+3.(2)证明见解析;(3)点P坐标为(![]() ,
, ![]() )或(2,3).
)或(2,3).
【解析】试题(1)将A(﹣1,0)、C(0,3),代入二次函数y=ax2+bx﹣3a,求得a、b的值即可确定二次函数的解析式;(2)分别求得线段BC、CD、BD的长,利用勾股定理的逆定理进行判定即可;(3)分以CD为底和以CD为腰两种情况讨论.运用两点间距离公式建立起P点横坐标和纵坐标之间的关系,再结合抛物线解析式即可求解.
试题解析:(1)∵二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),∴将A(﹣1,0)、C(0,3),代入,得![]() ,解得
,解得![]() ,∴抛物线的解析式为y=﹣x2+2x+3;(2)如图,连接DC、BC、DB,由y=﹣x2+2x+3=﹣(x﹣1)2+4得,D点坐标为(1,4),∴CD=
,∴抛物线的解析式为y=﹣x2+2x+3;(2)如图,连接DC、BC、DB,由y=﹣x2+2x+3=﹣(x﹣1)2+4得,D点坐标为(1,4),∴CD=![]() =
=![]() ,BC=
,BC=![]() =3
=3![]() ,BD=
,BD=![]() =2
=2![]() ,∵CD2+BC2=(
,∵CD2+BC2=(![]() )2+(3
)2+(3![]() )2=20,BD2=(2
)2=20,BD2=(2![]() )2=20,∴CD2+BC2=BD2,∴△BCD是直角三角形;(3)y=﹣x2+2x+3对称轴为直线x=1.假设存在这样的点P,①以CD为底边,则P1D=P1C,设P1点坐标为(x,y),根据勾股定理可得P1C2=x2+(3﹣y)2,P1D2=(x﹣1)2+(4﹣y)2,因此x2+(3﹣y)2=(x﹣1)2+(4﹣y)2,即y=4﹣x.又P1点(x,y)在抛物线上,∴4﹣x=﹣x2+2x+3,即x2﹣3x+1=0,解得x1=
)2=20,∴CD2+BC2=BD2,∴△BCD是直角三角形;(3)y=﹣x2+2x+3对称轴为直线x=1.假设存在这样的点P,①以CD为底边,则P1D=P1C,设P1点坐标为(x,y),根据勾股定理可得P1C2=x2+(3﹣y)2,P1D2=(x﹣1)2+(4﹣y)2,因此x2+(3﹣y)2=(x﹣1)2+(4﹣y)2,即y=4﹣x.又P1点(x,y)在抛物线上,∴4﹣x=﹣x2+2x+3,即x2﹣3x+1=0,解得x1=![]() ,x2=
,x2=![]() <1,(不满足在对称轴右侧应舍去),∴x=
<1,(不满足在对称轴右侧应舍去),∴x=![]() ,∴y=4﹣x=
,∴y=4﹣x=![]() ,即点P1坐标为(
,即点P1坐标为(![]() ,
, ![]() ).②以CD为一腰,∵点P2在对称轴右侧的抛物线上,由抛物线对称性知,点P2与点C关于直线x=1对称,此时点P2坐标为(2,3).∴符合条件的点P坐标为(
).②以CD为一腰,∵点P2在对称轴右侧的抛物线上,由抛物线对称性知,点P2与点C关于直线x=1对称,此时点P2坐标为(2,3).∴符合条件的点P坐标为(![]() ,
, ![]() )或(2,3).
)或(2,3).


科目:初中数学 来源: 题型:
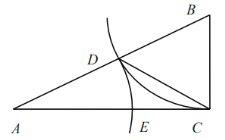
【题目】如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交边AB与点D,以A为圆心,AD长为半径画弧,交边AC于点E,连接CD.
(1)若∠A=28°,求∠ACD的度数;
(2)设BC=a,AC=b.
①线段AD的长是方程![]() 的一个根吗?为什么?
的一个根吗?为什么?
②若AD=EC,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
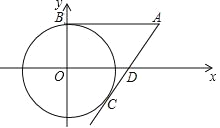
【题目】如图,在直角坐标系中,以点O为圆心,半径为4的圆与y轴交于点B,点A(8,4)是圆外一点,直线AC与⊙O切于点C,与x轴交于点D,则点C的坐标为( )
A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() )
)
C. (![]() ,
,![]() ) D. (
) D. (![]() ,-2)
,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
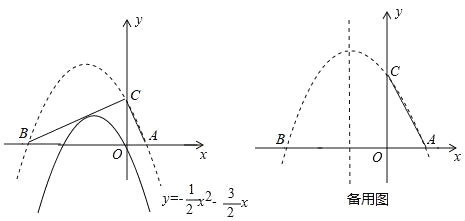
【题目】已知抛物线![]() 的图象如图所示:
的图象如图所示:
(1)将该抛物线向上平移2个单位,分别交x轴于A、B两点,交y轴于点C,则平移后的解析式为 .
(2)判断△ABC的形状,并说明理由.
(3)在抛物线对称轴上是否存在一点P,使得以A、C、P为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,井建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数P=![]() (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=![]()
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数解析式;
②该药厂销售部门分析认为,336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量P的最小值和最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
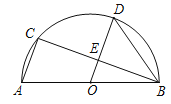
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两个点,且D是弧BC的中点,OD与BC交于点E,连接AC.
(1)若∠A=70°,求∠CBD的度数;
(2)若DE=2,BC=6,求半圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x2+(a+3)x+a+1=0是关于x的一元二次方程.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根为x1 ,x2 ,且x12+x22=10,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a>0)经过点A(-3![]() ,0)、B(
,0)、B(![]() ,0),它与y轴相交于点C,且∠ACB≥90°,设该抛物线的顶点为D,△BCD的边CD上的高为h.
,0),它与y轴相交于点C,且∠ACB≥90°,设该抛物线的顶点为D,△BCD的边CD上的高为h.
(1)求实数a的取值范围;
(2)求高h的取值范围;
(3)当(1)的实数a取得最大值时,求此时△BCD外接圆的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com